
【题目】已知全集![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)当a=1时,U=R,P={x|0<x<1},Q={x|﹣2≤x≤5},由此能求出UP和(UP)∩Q.
(2)由P={x|![]() a},Q={x|﹣2≤x≤5},P∩Q=P,得PQ,由此能求出实数a的取值范围.
a},Q={x|﹣2≤x≤5},P∩Q=P,得PQ,由此能求出实数a的取值范围.
(1)当a=1时,U=R,P={x|![]() 1}={x|0<x<1},
1}={x|0<x<1},
Q={x|x2﹣3x≤10}={x|﹣2≤x≤5}.
UP={x|x≤0或x≥1},
∴(UP)∩Q={x|﹣2≤x≤0或1≤x≤5}.
(2)∵P={x|![]() a},Q={x|﹣2≤x≤5},P∩Q=P,
a},Q={x|﹣2≤x≤5},P∩Q=P,
∴PQ,
当x>0时,P={x|0<x![]() },由PQ,得a
},由PQ,得a![]() ,
,
当x≤0时,PQ不成立.
综上,实数a的取值范围是[![]() ,+∞).
,+∞).


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,
,![]() ),
),![]() ,且函数
,且函数![]() 图像上的任意两条对称轴之间距离的最小值是
图像上的任意两条对称轴之间距离的最小值是![]() .
.
(1)求![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图像,求函数
的图像,求函数![]() 在
在![]() 上的最值,并求取得最值时的
上的最值,并求取得最值时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点(用t表示第t月份,![]() ),根据历年数据,某水库的蓄水量V(单位:亿立方米)与时间t的近似函数关系为:当0<t≤10时,
),根据历年数据,某水库的蓄水量V(单位:亿立方米)与时间t的近似函数关系为:当0<t≤10时,![]() ;当10<t≤12时,
;当10<t≤12时,![]() ;若2月份该水库的蓄水量为33.6亿立方米.
;若2月份该水库的蓄水量为33.6亿立方米.
(1)求实数a的值;
(2)求一年内该水库的最大蓄水量.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)是否存在非负整数![]() ,使得函数
,使得函数![]() 是单调函数,若存在,求出
是单调函数,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)已知![]() ,若存在
,若存在![]() ,使得当
,使得当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,求实数
,求实数![]() 的取值范围.(注:自然对数的底数
的取值范围.(注:自然对数的底数![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按
依次按![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项循环地分为
项循环地分为![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列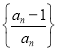 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com