
【题目】椭圆H: ![]() +y2=1(a>1),原点O到直线MN的距离为
+y2=1(a>1),原点O到直线MN的距离为 ![]() ,其中点M(0,﹣1),点N(a,0).
,其中点M(0,﹣1),点N(a,0).
(1)求该椭圆H的离心率e;
(2)经过椭圆右焦点F2的直线l和该椭圆交于A,B两点,点C在椭圆上,O为原点, 若 ![]() =
= ![]() +
+ ![]()
![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:直线MN的方程为: ![]() +
+ ![]() =1,即x﹣ay﹣a=0.∵
=1,即x﹣ay﹣a=0.∵ ![]() =
= ![]() ,解得a=
,解得a= ![]() .
.
又b=1,则 ![]() =
= ![]() .
.
∴该椭圆H的离心率e= ![]() =
= ![]() =
= ![]()
(2)解:由(1)可知:椭圆H的标准方程为: ![]() =1,设A(x1,y1),B(x2,y2).
=1,设A(x1,y1),B(x2,y2).
∵ ![]() =
= ![]() +
+ ![]()
![]() ,∴C
,∴C ![]() ,由A,B,C都在椭圆上,∴
,由A,B,C都在椭圆上,∴ ![]() =3,①
=3,① ![]() =3,②
=3,②  +3
+3  =3,③,由③化简整理可得:
=3,③,由③化简整理可得: ![]() (
( ![]() )+
)+ ![]() (
( ![]() )+
)+ ![]() (x1x2+3y1y2)=3,
(x1x2+3y1y2)=3,
把①②代入化简可得:x1x2+3y1y2=0,④.设直线l的方程为:x=my+ ![]() ,代入椭圆方程可得:(m2+3)y2+2
,代入椭圆方程可得:(m2+3)y2+2 ![]() my﹣1=0,∴y1+y2=
my﹣1=0,∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() +3,
+3,
∴x1x2= ![]() =m2y1y2+
=m2y1y2+ ![]() m(y1+y2)+2,
m(y1+y2)+2,
∴(m2+3)y1y2+ ![]() m(y1+y2)+2=0,
m(y1+y2)+2=0,
∴(m2+3) ![]() +
+ ![]() m
m ![]() +2=0,解得m=±1.
+2=0,解得m=±1.
∴直线l的方程为x=±y+ ![]() .
.
当直线l的斜率为0时,其方程为:y=0,此时A( ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0),不满足④,舍去.
,0),不满足④,舍去.
综上可得:直线l的方程为x=±y+ ![]()
【解析】(1)直线MN的方程为: ![]() +
+ ![]() =1,即x﹣ay﹣a=0.由
=1,即x﹣ay﹣a=0.由 ![]() =
= ![]() ,解得a=
,解得a= ![]() .利用
.利用 ![]() ,即可的得出.H的离心率e=
,即可的得出.H的离心率e= ![]() .(2)由(1)可知:椭圆H的标准方程为:
.(2)由(1)可知:椭圆H的标准方程为: ![]() =1,设A(x1 , y1),B(x2 , y2).由
=1,设A(x1 , y1),B(x2 , y2).由 ![]() =
= ![]() +
+ ![]()
![]() ,可得C
,可得C ![]() ,利用A,B,C都在椭圆上整理化简可得:x1x2+3y1y2=0.设直线l的方程为:x=my+
,利用A,B,C都在椭圆上整理化简可得:x1x2+3y1y2=0.设直线l的方程为:x=my+ ![]() ,代入椭圆方程可得:(m2+3)y2+2
,代入椭圆方程可得:(m2+3)y2+2 ![]() my﹣1=0,利用根与系数的关系代入可得m,对直线l的斜率为0时,直接验证即可.
my﹣1=0,利用根与系数的关系代入可得m,对直线l的斜率为0时,直接验证即可.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知中心在原点,焦点在x轴上的双曲线C的离心率为 ![]() ,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
(1)求双曲线C的方程及它的渐近线方程;
(2)求以直线l与坐标轴的交点为焦点的抛物线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知元素为实数的集合![]() 满足下列条件:①
满足下列条件:①![]() ,
, ![]() ;②若
;②若![]() ,则
,则![]() .
.
(I)若![]() ,求使元素个数最少的集合
,求使元素个数最少的集合![]() ;
;
(II)若非空集合![]() 为有限集,则你对集合
为有限集,则你对集合![]() 的元素个数有何猜测?并请证明你的猜测正确.
的元素个数有何猜测?并请证明你的猜测正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于![]() .
.
(1)求直线l的方程.
(2)求圆心在直线l上且经过点M(2,1),N(4,-1)的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序对
(天)组成有序对![]() ,点
,点![]() 落在右方图象中的两条线段上,该股票在30天内(包括30天)的日交易量
落在右方图象中的两条线段上,该股票在30天内(包括30天)的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的函数关系为:
(天)的函数关系为: ![]() ,
, ![]() ,
, ![]()
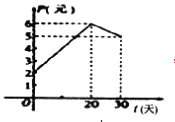
(1)根据提供的图象,写出该种股票每股的交易价格![]() (元)与时间
(元)与时间![]() (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)用![]() (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出![]() 关于
关于![]() 的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() , ①若f(a)=14,求a的值
, ①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为![]() ,
, ![]() ,
, ![]() (
(![]() ,且
,且![]() ,
, ![]() ,
, ![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com