
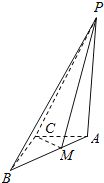
【题目】已知![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() ,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若
,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若![]() 平面ABC,则三棱锥
平面ABC,则三棱锥![]() 的四个面都是直角三角形;②若
的四个面都是直角三角形;②若![]() 平面ABC,且M是边AB的中点,则有
平面ABC,且M是边AB的中点,则有![]() ;③若
;③若![]() ,
,![]() 平面ABC,则
平面ABC,则![]() 面积的最小值为
面积的最小值为![]() ;④若
;④若![]() ,P在平面ABC上的射影是
,P在平面ABC上的射影是![]() 内切圆的圆心,则点P到平面ABC的距离为
内切圆的圆心,则点P到平面ABC的距离为![]() .其中正确命题的序号是________.(把你认为正确命题的序号都填上)
.其中正确命题的序号是________.(把你认为正确命题的序号都填上)
【答案】①②④
【解析】
①:利用勾股定理及逆定理和线面垂直的判定定理和性质定理可以判断本命题的真假;
②:根据直角三角形斜边的性质和勾股定理可以判断出本命题的真假;
③:利用面积公式和勾股定理可以判断出本命题的真假;
④:利用直角三角形内切圆的性质以及勾股定理可以判断出本命题的真假;
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]()
①:由上可知: ![]() 是直角三角形.
是直角三角形. ![]() 平面ABC,而
平面ABC,而![]() 平面ABC,因此
平面ABC,因此
![]() ,所以
,所以![]() 是直角三角形.因为
是直角三角形.因为
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,而
,而
![]() 平面
平面![]() ,所以
,所以![]() ,因此
,因此![]() 是直角三角形,故本命题是真命题;
是直角三角形,故本命题是真命题;
②:因为![]() 是以
是以![]() 为斜边的直角三角形, M是边AB的中点,所以
为斜边的直角三角形, M是边AB的中点,所以![]() ,
,
又![]() 平面ABC,
平面ABC, ![]() 平面ABC,所以
平面ABC,所以![]() ,由勾股定理可知:
,由勾股定理可知:
![]() ,而
,而![]() ,
,
所以![]() ,故本命题是真命题;
,故本命题是真命题;
③:![]() ,当
,当![]() 最小时,
最小时,![]() 面积有最小值,所以当
面积有最小值,所以当
![]() 时,此时
时,此时![]() ,所以
,所以![]() 面积最小值为6,故本命题是假命题;
面积最小值为6,故本命题是假命题;
④:由内切圆关径公式可知:内切圆的半径![]() ,故
,故![]() ,设P在平面ABC上的射影是
,设P在平面ABC上的射影是![]() 内切圆的圆心为O,因此有
内切圆的圆心为O,因此有![]() ,
,
所以![]() ,所以点P到平面ABC的距离为
,所以点P到平面ABC的距离为![]() .故本命题是真命题;
.故本命题是真命题;
故答案为:①②④


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价为每天180元时,房间会全部住满;房间单价增加10元,就会有一个房间空闲,如果游客居住房间,宾馆每间每天需花费20元的各种维护费用.房间定价多少时,宾馆利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,济南公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数, ![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表
表示每天使用扫码支付的人次(单位:十人次),统计数据如表![]() 所示:
所示:

根据以上数据,绘制了散点图.

(1)根据散点图判断,在推广期内, ![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表![]() 中的数据,建立
中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第
的回归方程,并预测活动推出第![]() 天使用扫码支付的 人次;
天使用扫码支付的 人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下

车队为缓解周边居民出行压力,以![]() 万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为
万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为![]() 万元.已知该线路公交车票价为
万元.已知该线路公交车票价为![]() 元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受
元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受![]() 折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有
折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠.预计该车队每辆车每个月有
折优惠.预计该车队每辆车每个月有![]() 万人次乘车,根据给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要
万人次乘车,根据给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要![]() 年才能开始盈利,求
年才能开始盈利,求![]() 的值.
的值.
参考数据:

其中其中![]()
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图像与
的图像与![]() 的图像有交点,求
的图像有交点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 最小值为1,若存在,求出
最小值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com