
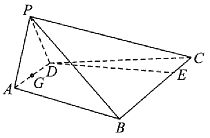
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由等腰梯形的性质可证得![]() ,由射影可得
,由射影可得![]() 平面
平面![]() ,进而求证;
,进而求证;
(2)取![]() 的中点F,连接
的中点F,连接![]() ,以G为原点,
,以G为原点,![]() 所在直线为x轴,
所在直线为x轴,![]() 所在直线为y轴,
所在直线为y轴,![]() 所在直线为z轴,建立空间直角坐标系,分别求得平面
所在直线为z轴,建立空间直角坐标系,分别求得平面![]() 与平面
与平面![]() 的法向量,再利用数量积求解即可.
的法向量,再利用数量积求解即可.
(1)在等腰梯形![]() 中,
中,
![]() 点E在线段
点E在线段![]() 上,且
上,且![]() ,
,
![]() 点E为
点E为![]() 上靠近C点的四等分点,
上靠近C点的四等分点,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
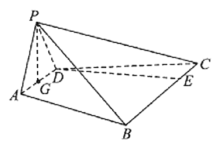
![]() 点P在底面
点P在底面![]() 上的射影为
上的射影为![]() 的中点G,连接
的中点G,连接![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)取![]() 的中点F,连接
的中点F,连接![]() ,以G为原点,
,以G为原点,![]() 所在直线为x轴,
所在直线为x轴,![]() 所在直线为y轴,
所在直线为y轴,![]() 所在直线为z轴,建立空间直角坐标系,如图所示,
所在直线为z轴,建立空间直角坐标系,如图所示,
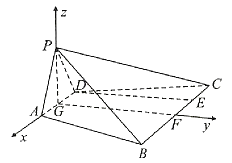
由(1)易知,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() 为等边三角形,
为等边三角形,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则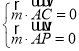 ,即
,即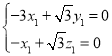 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则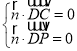 ,即
,即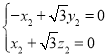 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 与平面
与平面![]() 的夹角为θ,则
的夹角为θ,则
![]()
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:
年龄( |
|
|
|
|
|
患病人数( |
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)计算变量![]() 、
、![]() 的相关系数
的相关系数![]() (计算结果精确到
(计算结果精确到![]() ),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若
),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若![]() ,则
,则![]() 、
、![]() 相关性很强;若
相关性很强;若![]() ,则
,则![]() 、
、![]() 相关性一般;若
相关性一般;若![]() ,则
,则![]() 、
、![]() 相关性较弱.)
相关性较弱.)
参考数据:![]() .
.
参考公式: ,
,
相关系数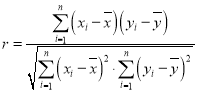 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,单位圆上有一点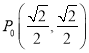 ,点
,点![]() 以点
以点![]() 为起点按逆时针方向以每秒
为起点按逆时针方向以每秒![]() 弧度作圆周运动,点
弧度作圆周运动,点![]() 的纵坐标
的纵坐标![]() 是关于时间
是关于时间![]() 的函数,记作
的函数,记作![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)若将函数![]() 向左平移
向左平移![]() 个单位长度后,得到的曲线关于
个单位长度后,得到的曲线关于![]() 轴对称,求
轴对称,求![]() 的最小正值,并求此时
的最小正值,并求此时![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
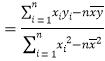 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为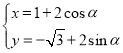 (其中
(其中![]() 为参数,
为参数,![]() ).在极坐标系(以坐标原点
).在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上恰有一个点到曲线
上恰有一个点到曲线![]() 的距离为1,求曲线
的距离为1,求曲线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com