
【题目】如图所示,在四棱台![]() 中,
中, ![]() 底面
底面![]() ,四边形
,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() .
.
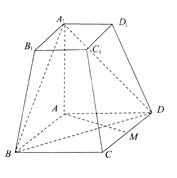
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】(Ⅰ)要证直线![]() 与平面
与平面![]() 垂直,现在由
垂直,现在由![]() 与底面垂直有
与底面垂直有![]() ,因此还要证一个垂直,证
,因此还要证一个垂直,证![]() ,这可通过等边三角形
,这可通过等边三角形![]() 得证
得证![]() ,从而有需要的结论
,从而有需要的结论![]() ,因此证得线面垂直;
,因此证得线面垂直;
(Ⅱ)要求直线与平面所成的角,分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
, ![]() 、
、![]() 、
、![]() 、
、 ,求出平面
,求出平面![]() 的法向量,由直线的方向向量与平面法向量夹角得线面角.
的法向量,由直线的方向向量与平面法向量夹角得线面角.
试题解析:(Ⅰ) ![]() 四边形为菱形,
四边形为菱形, ![]() ,连结
,连结![]() ,则
,则![]() 为等边三角形,
为等边三角形,
又![]() 为
为![]() 中点,
中点, ![]() ,由
,由![]() 得,
得, ![]() ,
,
![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,又
,又![]() ,
,
![]() 平面
平面![]()
(Ⅱ)![]() 四边形
四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,又
,又![]() 底面
底面![]() ,
,
分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
![]() 、
、![]() 、
、![]() 、
、 ,
,
 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有 ,令
,令![]() ,则
,则![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
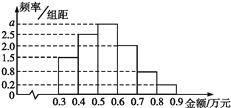
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是![]() ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是![]() ,问:
,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上不影响其存活的记号,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产![]() ,
, ![]() 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产![]() 类产品5件和
类产品5件和![]() 类产品10件,乙种设备每天能生产
类产品10件,乙种设备每天能生产![]() 类产品6件和
类产品6件和![]() 类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产
类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产![]() 类产品50件,
类产品50件, ![]() 类产品140件,则所需租赁费最少为__________元.
类产品140件,则所需租赁费最少为__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】媒体为调查喜欢娱乐节目![]() 是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
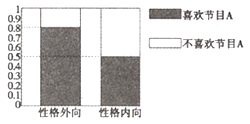
(1)填写完整如下![]() 列联表;
列联表;

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.001的前提下认为喜欢娱乐节目![]() 与性格外向有关?
与性格外向有关?
参考数据及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
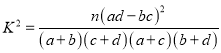
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com