
【题目】已知函数f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函数图象的对称中心到对称轴的最小距离为
)+b(ω>0),且函数图象的对称中心到对称轴的最小距离为 ![]() ,当x∈[0,
,当x∈[0, ![]() ]时,f(x)的最大值为1.
]时,f(x)的最大值为1.
(1)求函数f(x)的解析式;
(2)将函数f(x)的图象向右平移 ![]() 个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0,
个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
【答案】
(1)解:∵函数f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函数图象的对称中心到对称轴的最小距离为
)+b(ω>0),且函数图象的对称中心到对称轴的最小距离为 ![]() ,
,
∴ ![]() =
= ![]() ,可得:T=π,由
,可得:T=π,由 ![]() =π,可得:ω=2,
=π,可得:ω=2,
∴f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )+b,
)+b,
∵当x∈[0, ![]() ]时,2x﹣
]时,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴由于y=sinx在[﹣ ![]() ,
, ![]() ]上单调递增,可得当2x﹣
]上单调递增,可得当2x﹣ ![]() =
= ![]() ,即x=
,即x= ![]() 时,函数f(x)取得最大值f(
时,函数f(x)取得最大值f( ![]() )=
)= ![]() sin
sin ![]() +b,
+b,
∴ ![]() sin
sin ![]() +b=1,解得b=﹣
+b=1,解得b=﹣ ![]() ,
,
∴f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣
)﹣ ![]()
(2)解:将函数f(x)的图象向右平移 ![]() 个单位长度得到函数解析式为:g(x)=
个单位长度得到函数解析式为:g(x)= ![]() sin[2(x﹣
sin[2(x﹣ ![]() )﹣
)﹣ ![]() ]﹣
]﹣ ![]() =
= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣
)﹣ ![]() ,
,
∵当x∈[0, ![]() ]时,可得:2x﹣
]时,可得:2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],g(x)=
],g(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣
)﹣ ![]() ∈[﹣2,1],
∈[﹣2,1],
∴g(x)﹣3∈[﹣5,﹣2],g(x)+3∈[1,4],
∵g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,
]上恒成立,
∴m∈[﹣5,4].
【解析】(1)由题意可求T=π,利用周期公式可求ω的值,可得解析式f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )+b,结合范围2x﹣
)+b,结合范围2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],利用正弦函数的有界性解得b的值,从而可求函数f(x)的解析式.(2)利用函数y=Asin(ωx+φ)的图象变换可求g(x)=
],利用正弦函数的有界性解得b的值,从而可求函数f(x)的解析式.(2)利用函数y=Asin(ωx+φ)的图象变换可求g(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣
)﹣ ![]() ,结合范围2x﹣
,结合范围2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],可求范围g(x)=
],可求范围g(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣
)﹣ ![]() ∈[﹣2,1],结合已知可求m的取值范围.
∈[﹣2,1],结合已知可求m的取值范围.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知曲线C上的动点P(![]() )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为![]()
(1)求曲线C的方程。
(2)过点M(1,2)的直线![]() 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).∠BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=3km. 
(1)求道路BE的长度;
(2)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项等比数列{an},若2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+log3a3+…log3an , 求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若互不相等的实数x1 , x2 , x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
,若互不相等的实数x1 , x2 , x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
A.( ![]() ]
]
B.( ![]() )
)
C.( ![]() ]
]
D.( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
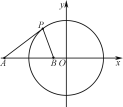
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com