
【题目】如图甲所示,![]() 是梯形
是梯形![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,先将梯形
,先将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() .
.
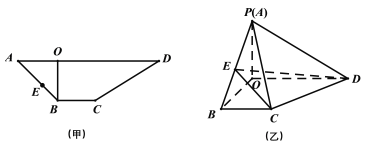
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)点![]() 是线段
是线段![]() 上一动点,当直线
上一动点,当直线![]() 与
与![]() 所成的角最小时,求二面角
所成的角最小时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,详见解析(2)
,详见解析(2)![]()
【解析】
(1)过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,易得
,易得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ,所以得到
,所以得到![]() 平面
平面![]() ,而此时根据几何关系可以得到
,而此时根据几何关系可以得到![]() ;(2)以
;(2)以![]() 为坐标原点建立空间直角坐标系,
为坐标原点建立空间直角坐标系,![]() ,表示出
,表示出![]() 与
与![]() 所成角为
所成角为![]() 的余弦值,并求出
的余弦值,并求出![]() 最小时
最小时![]() 的值,从而得到各点坐标,再求出平面
的值,从而得到各点坐标,再求出平面![]() 和平面
和平面![]() 的法向量,根据两个法向量之间的夹角公式,求得答案.
的法向量,根据两个法向量之间的夹角公式,求得答案.
解:(1)存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,理由如下:
,理由如下:
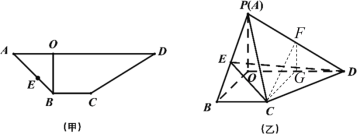
依题,![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() ,
,![]()
所以![]() ,
,
所以![]() ,
,
而![]() ,所以有
,所以有![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
而![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
故存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]()
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
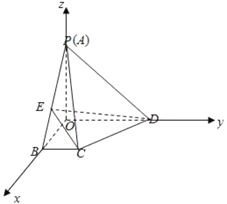
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]()
即![]() ,所以
,所以![]() ,
,
![]() ,
,![]()
设直线![]() 与
与![]() 所成角为
所成角为![]()
则![]()
令![]() ,则
,则![]() ,
,
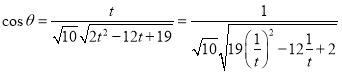
令![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() 取最大值,
取最大值,
此时直线![]() 与
与![]() 所成的角最小.此时
所成的角最小.此时![]() .
.
所以![]() ,又因为
,又因为![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 法向量分别为
法向量分别为![]()
则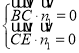 ,即
,即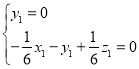
取![]() 得平面
得平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 法向量为
法向量为![]()
则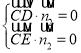 ,即
,即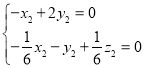
取![]() 得平面
得平面![]() 法向量为
法向量为![]()
所以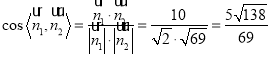 ,
,
由图可知,二面角![]() 为钝二面角,则其余弦值为
为钝二面角,则其余弦值为![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①正切函数图象的对称中心是唯一的;
②若函数![]() 的图像关于直线
的图像关于直线![]() 对称,则这样的函数
对称,则这样的函数![]() 是不唯一的;
是不唯一的;
③若![]() ,
,![]() 是第一象限角,且
是第一象限角,且![]() ,则
,则![]() ;
;
④若![]() 是定义在
是定义在![]() 上的奇函数,它的最小正周期是
上的奇函数,它的最小正周期是![]() ,则
,则![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com