
【题目】已知等腰梯形![]() ,
,![]() .现将
.现将![]() 沿着
沿着![]() 折起,使得面
折起,使得面![]() 面
面![]() ,点F为线段BC上一动点.
,点F为线段BC上一动点.
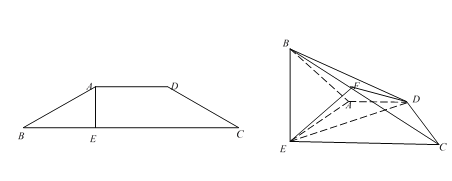
(1)证明:![]() ;
;
(2)如果F为BC中点,证明:![]() 面
面![]() ;
;
(3)若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)先通过面![]() 面
面![]() 得到
得到![]() 面
面![]() ,进而可得
,进而可得![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,通过证明四边形
,通过证明四边形![]() 为平行四边形,得到
为平行四边形,得到![]() ,进而可得
,进而可得![]() 面
面![]() ;
;
(3)以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设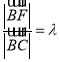 求出面
求出面![]() 的法向量和面
的法向量和面![]() 的法向量,通过二面角
的法向量,通过二面角![]() 的余弦值为
的余弦值为![]() 列方程求出
列方程求出![]() ,即
,即![]() 的值.
的值.
(1)证明:在等腰梯形中,![]() 所以
所以![]() ,
,
因为面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
所以![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
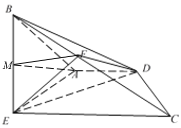
在三角形![]() 中,
中,![]() 而
而![]() ,所以
,所以![]() ,
,
即四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
因为![]() 面
面![]() 面
面![]() 所以
所以![]() 面
面![]() ;
;
(3)由![]() 面
面![]() ,
,![]() 则以
则以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
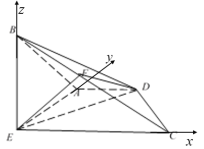
则![]() ,
,![]() ,
,
设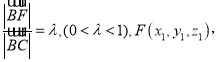 则
则![]() ,
,
设面![]() 的法向量
的法向量![]() ,
,
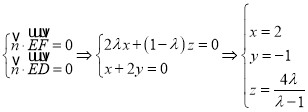 ,即
,即![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 是面
是面![]() 的法向量,
的法向量,
若二面角![]() 的余弦值为
的余弦值为![]() ,
,
则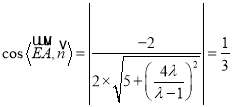 ,
,
解得![]() 或者
或者![]() ,由题意
,由题意![]() ,
,
即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
C. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D. 若命题“![]() ”为假命题,则命题
”为假命题,则命题![]() ,
,![]() 都是假命题
都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为征求个人所得税法修改建议,某机构对当地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).
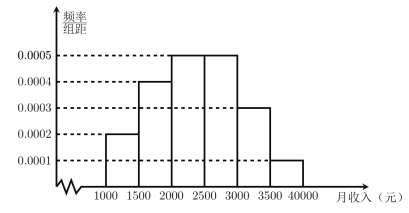
(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图估算样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知双曲线与椭圆![]() 有相同焦点,且过点
有相同焦点,且过点![]() ,求双曲线标准方程;
,求双曲线标准方程;
(2)已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,椭圆上一点
,椭圆上一点![]() 到焦点
到焦点![]() 的最大距离是3,求这个椭圆的离心率.
的最大距离是3,求这个椭圆的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)若![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 必可以被分为1组或2组,使得每组所有数的和小于1;
必可以被分为1组或2组,使得每组所有数的和小于1;
(2)若![]() ,求证:
,求证:![]() ,
,![]() …,
…,![]() ,必可以被分为
,必可以被分为![]() 组
组![]() ,使得每组所有数的和小于1.
,使得每组所有数的和小于1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com