设{an}是单调递增的等差数列,Sn为其前n项和,且满足4S3=S6,a2+2是a1,a13的等比中项.
(I)求数列{an}的通项公式;
(II)是否存在m,k∈N*,使am+am+4=ak+2?说明理由;
(III)若数列{bn}满足b1=-1,bn+1-bn=an,求数列{bn}的通项公式.
【答案】
分析:(I)设公差为d(d>0),利用4S
3=S
6,a
2+2是a
1,a
13的等比中项,建立方程组,求出首项与公差,即可求数列{a
n}的通项公式;
(II)假设存在m,k∈N
*,使a
m+a
m+4=a
k+2,利用通项可得等式,结合m,k∈N
*,即可得到结论;
(III)利用叠加法,即可求数列{b
n}的通项公式.
解答:解:(I)设公差为d(d>0),则
∵4S
3=S
6,a
2+2是a
1,a
13的等比中项,
∴

∴
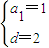
或
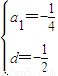
∵d>0,∴
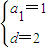
∴数列{a
n}的通项公式a
n=2n-1;
(II)若存在m,k∈N
*,使a
m+a
m+4=a
k+2,则2m-1+2(m+4)-1=2(k+2)-1,即2k-4m=3
∴k-2m=

∵m,k∈N
*,∴k-2m=

不可能成立
∴不存在m,k∈N
*,使a
m+a
m+4=a
k+2;
(III)由题意可得b
2-b
1=1,b
3-b
2=3,b
n-b
n-1=2n-3
将上面n-1个式子相加可得b
n-b
1=
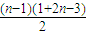
=(n-1)
2∵b
1=-1,∴

.
点评:本题考查数列的通项,考查叠加法的运用,考查学生分析解决问题的能力,属于中档题.


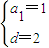 或
或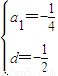
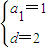

 不可能成立
不可能成立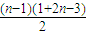 =(n-1)2
=(n-1)2 .
.
