
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上![]() 件产品作为样本算出他们的重量(单位:克)重量的分组区间为
件产品作为样本算出他们的重量(单位:克)重量的分组区间为![]() ,
,![]() ,……
,……![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
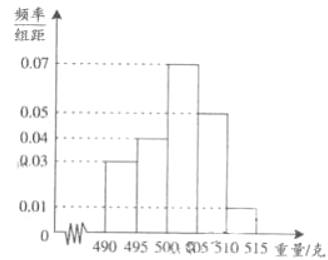
(1)根据频率分布直方图,求重量超过![]() 克的产品数量.
克的产品数量.
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列.
的分布列.
(3)从流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品合格的重量超过
件产品合格的重量超过![]() 克的概率.
克的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是底面边长为1的正三棱锥,
是底面边长为1的正三棱锥,![]() 分别为棱长
分别为棱长![]() 上的点,截面
上的点,截面![]() 底面
底面![]() ,且棱台
,且棱台![]() 与棱锥
与棱锥![]() 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

(1)证明:![]() 为正四面体;
为正四面体;
(2)若![]() ,求二面角
,求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(3)设棱台![]() 的体积为
的体积为![]() ,是否存在体积为
,是否存在体积为![]() 且各棱长均相等的直平行六面体,使得它与棱台
且各棱长均相等的直平行六面体,使得它与棱台![]() 有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
(注:用平行于底的截面截棱锥,该截面与底面之间的部分称为棱台,本题中棱台的体积等于棱锥![]() 的体积减去棱锥
的体积减去棱锥![]() 的体积.)
的体积.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() 的斜率
的斜率![]() 满足
满足![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.

(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,设实数
,设实数![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足
(i)![]() 、
、![]() 、
、![]() 且不全为0;
且不全为0;
(ii)![]() 、
、![]() 、
、![]() ;
;
(iii)若![]() ,则
,则![]() .
.
若所有形如![]() 和
和![]() 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合![]() 为“好集”.求好集
为“好集”.求好集![]() 所含元素个数的最大值.
所含元素个数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com