
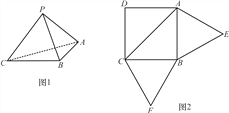
【题目】已知三棱锥![]() (如图
(如图![]() )的平面展开图(如图
)的平面展开图(如图![]() )中,四边形
)中,四边形![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
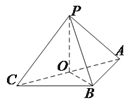
【解析】分析:(1)设AC的中点为O,连接BO,PO.推导出PO⊥AC,PO⊥OB,从而 PO⊥平面ABC,由此能证明平面PAC⊥平面ABC.
(2)由PO⊥平面ABC,OB⊥AC,建立空间直角坐标系,利用向量法能求出二面角A﹣PC﹣B的余弦值.
详解:(1)证明:
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .由题意得,
.由题意得,
![]() ,
,![]() ,
,![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
(2)解:由![]() 平面
平面![]() ,
,![]() ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则
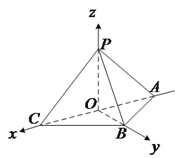
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由![]() 平面
平面![]() ,故平面
,故平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由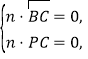 得:
得:![]()
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,
,
![]() .
.
由二面角![]() 是锐二面角,
是锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某公司在某条商业街分别开有两家业务上有关联的零售商店,这两家商店的日纯利润变化情况如下表所示:

(1)从这几天的日纯利润来看,哪一家商店的日平均纯利润多些?
(2)由表中数据可以认为这两家商店的日纯利润之间有较强的线性相关关系.
(ⅰ)试求![]() 与
与![]() 之间的线性回归方程;
之间的线性回归方程;
(ⅱ)预测当![]() 店日纯利润不低于2万元时,
店日纯利润不低于2万元时,![]() 店日纯利润的大致范围(精确到小数点后两位);
店日纯利润的大致范围(精确到小数点后两位);
(3)根据上述5日内的日纯利润变化情况来看,哪家商店经营状况更好?
附:线性回归方程![]() 中,
中,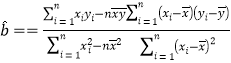 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①终边在y轴上的角的集合是{β|β=![]() }
}
②设一扇形的弧长为4cm,面积为4cm2,则这个扇形的圆心角的弧度数是2
③![]() 时,
时,![]()
④函数y=x2的图像与函数y=|lgx|的图像的交点个数为2个
所有正确命题的序号是______. (把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上且
上且![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点, ![]() ,
, ![]() 为椭圆
为椭圆![]() 的上顶点,
的上顶点, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() ,且满足
,且满足![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为研究学生玩电脑游戏和对待作业量态度的关系,随机抽取了100名学生进行调查,所得数据如下表所示:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 25 | 15 | 40 |
不喜欢玩电脑游戏 | 25 | 35 | 60 |
总计 | 50 | 50 | 100 |
(参考公式![]() ,可能用到数据:
,可能用到数据:![]() ,
,![]() ),参照以上公式和数据,得到的正确结论是( )
),参照以上公式和数据,得到的正确结论是( )
A. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
B. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
C. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
D. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家水果店的店长为了解本店苹果的日销售情况,记录了过去30天苹果的日销售量(单位:kg),结果如下:
83,96,107,91,70,75,94,80,80,100,
75,99,117,89,74,94,84,85,101,87.
93,85,107,99,55,97,86,84,85,104
(1)请计算该水果店过去30天苹果日销售量的中位数、平均数、极差和标准差
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),请问,每天应该进多少千克苹果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位年会进行抽奖活动,在抽奖箱里装有![]() 张印有“一等奖”的卡片,
张印有“一等奖”的卡片, ![]() 张印
张印
有“二等奖”的卡片, 3张印有“新年快乐”的卡片,抽中“一等奖”获奖![]() 元, 抽中“二等奖”获奖
元, 抽中“二等奖”获奖![]() 元,抽中“新年快乐”无奖金.
元,抽中“新年快乐”无奖金.
(1)单位员工小张参加抽奖活动,每次随机抽取一张卡片,抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记![]() 表示“小张恰好抽奖
表示“小张恰好抽奖![]() 次停止活动”,求
次停止活动”,求![]() 的值;
的值;
(2)若单位员工小王参加抽奖活动,一次随机抽取![]() 张卡片.
张卡片.
①![]() 记
记![]() 表示“小王参加抽奖活动中奖”,求
表示“小王参加抽奖活动中奖”,求![]() 的值;
的值;
②设![]() 表示“小王参加抽奖活动所获奖金数(单位:元)”,求
表示“小王参加抽奖活动所获奖金数(单位:元)”,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com