Question

【题目】在直角坐标系中，椭圆 的左、右焦点分别为，点在椭圆上且轴，直线交轴于点， ， 为椭圆的上顶点， 的面积为1.

（1）求椭圆的方程；

（2）过的直线交椭圆于， ，且满足，求的面积.

Answer 1

【答案】（1）；（2）

【解析】【试题分析】(1)将代入椭圆方程,求得点的纵坐标,利用中点的坐标建立一个方程.利用的面积联立第二个方程,结合,解方程组求得的值,即求得椭圆的方程.(2)对两边平方化简得.当直线斜率不存在时,求得两点的坐标,验证可知不符合题意.当直线斜率存在时,设出直线方程,联立直线方程和椭圆的方程,消去后斜率韦达定理,利用得,列方程求得直线的斜率.最后利用弦长公式和点到直线距离公式求得三角形面积.

【试题解析】

（1）设，由题意可得，即.

∵是的中位线，且，∴，即，整理得.①

又由题知， 为椭圆的上顶点，∴的面积，

整理得，即，②

联立①②可得，变形得，解得，进而.

∴椭圆的方程为.

(2)由可得，两边平方整理得.

直线斜率不存在时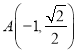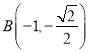， ， ，不满足.

直线斜率存在时，设直线的方程为， ， ，

联立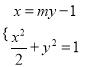，消去，得，

∴， ，（*）

由得.

将， 代入整理得，

展开得，

将（*）式代入整理得，解得，

∴， ，

的面积为 ，

代入计算得，即的面积为.