
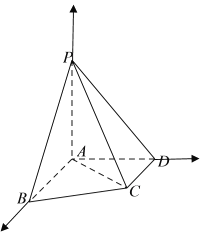
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() .
.

(![]() )求二面角
)求二面角![]() 的正弦值.
的正弦值.
(![]() )设点
)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(![]() )
)![]() .(
.(![]() )
)![]() .
.
【解析】
先由题意得到![]() 两两垂直;以
两两垂直;以![]() 为坐标原点,
为坐标原点,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向,建立空间直角坐标系;
轴正方向,建立空间直角坐标系;
(1)分别求出平面![]() ,平面
,平面![]() 的法向量,根据向量夹角余弦值,即可求出结果;
的法向量,根据向量夹角余弦值,即可求出结果;
(2)先设![]() ,
,![]() ,根据题中条件,用
,根据题中条件,用![]() 表示出
表示出![]() 点坐标,再由线面角的正弦值,即可列出等式,求出结果.
点坐标,再由线面角的正弦值,即可列出等式,求出结果.
因为![]() ,
,![]() 平面
平面![]() ,所以,易得
,所以,易得![]() 两两垂直;以
两两垂直;以![]() 为坐标原点,
为坐标原点,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向,建立如图所示空间直角坐标系;
轴正方向,建立如图所示空间直角坐标系;
则![]() ,
,![]() ,
,![]() ,
,![]()
(![]() )因此
)因此![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ;
;
所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则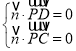 即
即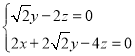 ,所以
,所以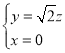
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
∴二面角![]() 正弦值为
正弦值为![]() .
.
(![]() )设
)设![]() ,
,![]() ,
,
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() ,
,
即![]() ,
,
得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
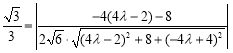 ,
,
得![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程和C2的直角坐标方程;
(2)射线OP:![]() (其中
(其中![]() )与C2交于P点,射线OQ:
)与C2交于P点,射线OQ:![]() 与C2交于Q点,求
与C2交于Q点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?
时,日销售额是多少?
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
线性回归方程![]() 中,
中,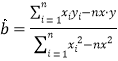 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com