Question

【题目】已知两定点， ，曲线上的动点满足，直线与曲线的另一个交点为．

（Ⅰ）求曲线的标准方程；

（Ⅱ）设点，若，求直线的方程．

Answer 1

【答案】（Ⅰ）（Ⅱ）

【解析】试题分析：（Ⅰ）由题意知|MF1|+|MF2|=2|F1F2|=8＞4，所以曲线C是以F1，F2为焦点，长轴长为8的椭圆．由此可知曲线C的方程；（Ⅱ）设M（xM，yM），P（xP，yP），直线MN方程为y=k（x+4），其中k≠0．由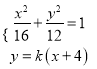得（3+4k2）y2-24ky=0，由此利用韦达定理、椭圆性质，结合已知条件，所以，则，转化为坐标关系求出点坐标代入椭圆即可.

试题解析：

（Ⅰ）∵， ，

∴，

∵，

∴曲线是以， 为焦点，长轴长为的椭圆．

曲线的方程为．

（Ⅱ）由题意知直线不垂直于轴，也不与轴重合或平行．

设， ，直线方程为，其中．

由，得．

解得或．

依题意， ．

因为，

所以，则．

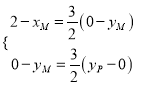于是，所以，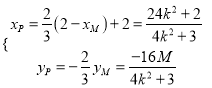

因为点在椭圆上，所以．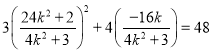

整理得，

解得或（舍去），

从而．

所以直线的方程为．