
【题目】已知抛物线![]() 过点
过点![]() ,该抛物线的准线与椭圆
,该抛物线的准线与椭圆![]() :
:![]() 相切,且椭圆的离心率为
相切,且椭圆的离心率为![]() ,点
,点![]() 为椭圆
为椭圆![]() 的右焦点.
的右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]()
![]() 两点,
两点,![]() 为平面上一定点,且满足
为平面上一定点,且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)将点![]() 代入抛物线方程可得
代入抛物线方程可得![]() ,即可得到准线方程,又由于椭圆相切可得
,即可得到准线方程,又由于椭圆相切可得![]() ,再利用椭圆的离心率求得
,再利用椭圆的离心率求得![]() ,进而求解;
,进而求解;
(2)分别讨论直线![]() 斜率为0与直线
斜率为0与直线![]() 斜率不为0的情况,利用斜率公式处理
斜率不为0的情况,利用斜率公式处理![]() ,对于直线
,对于直线![]() 斜率不为0的情况,设直线
斜率不为0的情况,设直线![]() 为
为![]() ,联立直线
,联立直线![]() 与椭圆方程,由韦达定理可得
与椭圆方程,由韦达定理可得![]() 的关系,代入
的关系,代入![]() 中即可求解.
中即可求解.
(1)![]() 抛物线
抛物线![]() 过点
过点![]() ,
,![]() ,即
,即![]() ,
,
∴抛物线的准线为![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1),右焦点![]() ,
,
若直线![]() 斜率为0,则不妨设
斜率为0,则不妨设![]() ,
,![]() ,
,
∴![]() ,满足条件,此时直线
,满足条件,此时直线![]() 的方程为
的方程为![]() ;
;
若直线![]() 的斜率不为0,设
的斜率不为0,设![]() 的方程为
的方程为![]() ,
,
与椭圆的方程联立得:![]() ,可得
,可得![]() 恒成立,
恒成立,
设![]() ,
,![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,①
,①
∴![]()
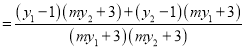
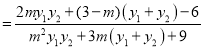 ,
,
将①代入得![]() ,解得
,解得![]() ,
,
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂![]() ,
,![]() 两条相互独立的生产线生产同款产品,在产量一样的情况下通过日常监控得知
两条相互独立的生产线生产同款产品,在产量一样的情况下通过日常监控得知![]() ,
,![]() 生产线生产的产品为合格品的概率分别为
生产线生产的产品为合格品的概率分别为![]() 和
和![]() .
.
(1)从![]() ,
,![]() 生产线上各抽检一件产品,若使得至少有一件合格的概率不低于
生产线上各抽检一件产品,若使得至少有一件合格的概率不低于![]() ,求
,求![]() 的最小值
的最小值![]() .
.
(2)假设不合格的产品均可进行返工修复为合格品,以(1)中确定的![]() 作为
作为![]() 的值.
的值.
①已知![]() ,
,![]() 生产线的不合格产品返工后每件产品可分别挽回损失
生产线的不合格产品返工后每件产品可分别挽回损失![]() 元和
元和![]() 元。若从两条生产线上各随机抽检
元。若从两条生产线上各随机抽检![]() 件产品,以挽回损失的平均数为判断依据,估计哪条生产线挽回的损失较多?
件产品,以挽回损失的平均数为判断依据,估计哪条生产线挽回的损失较多?
②若最终的合格品(包括返工修复后的合格品)按照一、二、三等级分类后,每件分别获利![]() 元、
元、![]() 元、
元、![]() 元,现从
元,现从![]() ,
,![]() 生产线的最终合格品中各随机抽取
生产线的最终合格品中各随机抽取![]() 件进行检测,结果统计如下图;用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为
件进行检测,结果统计如下图;用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为![]() ,求
,求![]() 的分布列并估算该厂产量
的分布列并估算该厂产量![]() 件时利润的期望值.
件时利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局公布的2013-2018年入境游客(单位:万人次)的变化情况,则下列结论错误的是( )

A.2014年我国入境游客万人次最少
B.后4年我国入境游客万人次呈逐渐增加趋势
C.这6年我国入境游客万人次的中位数大于13340万人次
D.前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
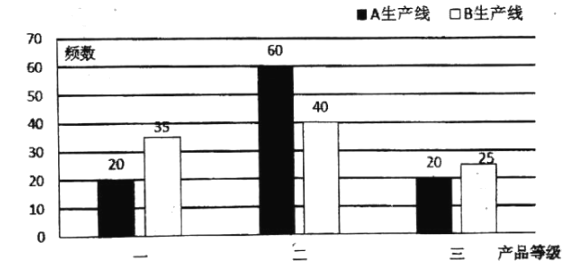
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是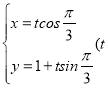 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是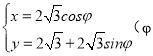 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,射线
两点,射线![]() 与直线
与直线![]() 交于
交于![]() 点,若
点,若![]() 的面积为1,求
的面积为1,求![]() 的值和弦长
的值和弦长![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() ,
,![]() 成等比数列,求直线
成等比数列,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“p且![]() ”为假命题,则p、q均为假命题;②命题“若a>b,则
”为假命题,则p、q均为假命题;②命题“若a>b,则![]() ”的否命题为“若a≤b,则
”的否命题为“若a≤b,则![]() ”;③“x∈R,
”;③“x∈R,![]() 的否定是“
的否定是“![]() ”;④在△ABC中,“A>B”是“
”;④在△ABC中,“A>B”是“![]() ”的充要条件;其中正确的命题的个数是( )
”的充要条件;其中正确的命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com