
【题目】已知函数![]() ,
,![]() ,其中a为常数,且曲线
,其中a为常数,且曲线![]() 在其与y轴的交点处的切线记为
在其与y轴的交点处的切线记为![]() ,曲线
,曲线![]() 在其与x轴的交点处的切线记为
在其与x轴的交点处的切线记为![]() ,且
,且![]() .
.
![]() 求
求![]() ,
,![]() 之间的距离;
之间的距离;
![]() 若存在x使不等式
若存在x使不等式![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
![]() 对于函数
对于函数![]() 和
和![]() 的公共定义域中的任意实数
的公共定义域中的任意实数![]() ,称
,称![]() 的值为两函数在
的值为两函数在![]() 处的偏差
处的偏差![]() 求证:函数
求证:函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
【答案】(1)![]() (2)
(2)![]() (3)见证明
(3)见证明
【解析】
![]() 求出函数的导数,结合题意求出a的值,求出
求出函数的导数,结合题意求出a的值,求出![]() ,
,![]() 的解析式,求出平行线间的距离即可;
的解析式,求出平行线间的距离即可;![]() 令
令![]() ,问题转化为
,问题转化为![]() ,求出m的范围即可;
,求出m的范围即可;
![]() 法一:令
法一:令![]() ,
,![]() ,求出函数的导数,根据函数的单调性求出
,求出函数的导数,根据函数的单调性求出![]() 的最小值,证明即可;法二:令
的最小值,证明即可;法二:令![]() ,
,![]() ,令
,令![]() ,
,![]() ;令
;令![]() ,
,![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
![]() ,
,![]() ,
,
![]() 的图象与坐标轴的交点为
的图象与坐标轴的交点为![]() ,
,
![]() 的图象与坐标轴的交点为
的图象与坐标轴的交点为![]() ,
,
由题意得![]() ,即
,即![]() ,
,
又![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 函数
函数![]() 和
和![]() 的图象在其坐标轴的交点处的切线方程分别为:
的图象在其坐标轴的交点处的切线方程分别为:
![]() ,
,![]() ,
,
![]() 两平行切线间的距离为
两平行切线间的距离为![]()
![]() 由
由![]() ,得
,得![]() ,
,
故![]() 在
在![]() 有解,
有解,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
故![]() ,
,
即![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() ,
,![]() ,
,
即实数m的取值范围为![]()
![]() 解法一:
解法一:
![]() 函数
函数![]() 和
和![]() 的偏差为:
的偏差为:![]() ,
,![]() ,
,
![]() ,设
,设![]() 为
为![]() 的解,则
的解,则![]()
则当![]() ,
,![]() ;当
;当![]() ,
,![]() ,
,
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故F![]() ,
,
即函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于
在其公共定义域内的所有偏差都大于![]()
解法二:
由于函数![]() 和
和![]() 的偏差:
的偏差:![]() ,
,![]() ,
,
令![]() ,
,![]() ;令
;令![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ,
,![]() ,
,
![]() ,
,
即函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于
在其公共定义域内的所有偏差都大于![]()


科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与椭圆
与椭圆![]() 交于A,B两点,点P是椭圆C上异于A,B的一个动点,点Q在直线AB上,满足
交于A,B两点,点P是椭圆C上异于A,B的一个动点,点Q在直线AB上,满足![]() (
(![]() 为坐标原点)
为坐标原点)
(1)求点Q的轨迹方程;
(2)求四边形OAPB的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆![]() 与双曲线
与双曲线![]() (
(![]() ,
,![]() )有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过
)有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过![]() 次反射后,首次回到左焦点所经过的路径长为______.
次反射后,首次回到左焦点所经过的路径长为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知过点![]() 的动直线与椭圆
的动直线与椭圆![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的面积S的取值范围.
的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l:![]() ,圆C:
,圆C:![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.直线l与圆C有可能无公共点
B.若直线l的一个方向向量为![]() ,则
,则![]()
C.若直线l平分圆C的周长,则![]()
D.若直线l与圆C有两个不同交点M、N,则线段MN的长的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
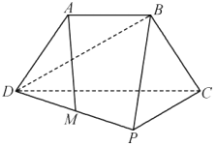
【题目】如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=![]() CD,AB∥CD,CP⊥CD,M为PD的中点.
CD,AB∥CD,CP⊥CD,M为PD的中点.
(1)求证:AM∥平面PBC;
(2)求证:BD⊥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据如图给出的2005年至2016年我国人口总量及增长率的统计图,以下结论不正确的是![]()
![]()
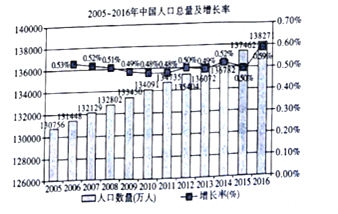
A. 自2005年以来,我国人口总量呈不断增加趋势
B. 自2005年以来,我国人口增长率维持在![]() 上下波动
上下波动
C. 从2005年后逐年比较,我国人口增长率在2016年增长幅度最大
D. 可以肯定,在2015年以后,我国人口增长率将逐年变大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com