【题目】已知函数
是定义在
上的奇函数，且当
时， 
；
（1）求函数
在
上的解析式并画出函数
的图象（不要求列表描点，只要求画出草图）
（2）（ⅰ）写出函数
的单调递增区间；
（ⅱ）若方程
在
上有两个不同的实数根，求实数
的取值范围。
百年学典课时学练测系列答案科目：高中数学 来源： 题型：
【题目】已知函数f(x)是正比例函数，函数g(x)是反比例函数，且f(1)＝1，g(1)＝2.
(1)求函数f(x)和g(x)；
(2)判断函数f(x)＋g(x)的奇偶性；
(3)求函数f(x)＋g(x)在(0，
]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有 
个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，
约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为 
或 
的人去参加
甲游戏，掷出点数大于 
的人去参加乙游戏．
（1）求这 
个人中恰有 
个人去参加甲游戏的概率；
（2）求这 
个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）当
时，求函数
在
上的最大值；
（2）令
，若
在区间
上为单调递增函数，求
的取值范围；
（3）当时，函数
的图象与
轴交于两点
且
，又
是
的导函数.若正常数
满足条件
.证明：
<0.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ax2－2ax＋2＋b(a≠0)在区间[2，3]上有最大值5，最小值2.
(1)求a，b的值；
(2)若b＜1，g(x)＝f(x)－2mx在[2，4]上单调，求m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于
的方程
，给出下列四个判断：
①存在实数
，使得方程恰有4个不同的实根；
②存在实数
，使得方程恰有5个不同的实根；
③存在实数
，使得方程恰有6个不同的实根；
④存在实数
，使得方程恰有8个不同的实根；
其中正确的为________（写出所有判断正确的序号）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当
时，证明函数
在
是单调函数；
（2）当
时，函数在区间
上的最小值是
，求
的值；
（3）设
，
是函数
图象上任意不同的两点，记线段
的中点的横坐标是
，证明直线的斜率
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正三棱柱ABCA1B1C1中，F，F1分别是AC，A1C1的中点．
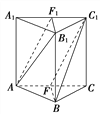
求证：(1)平面AB1F1∥平面C1BF；
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目：高中数学 来源： 题型：
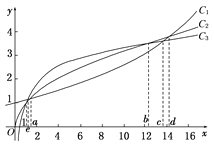
【题目】函数f(x)＝1.1x，g(x)＝ln x＋1，h(x)＝x
的图象如图所示，试分别指出各曲线对应的函数，并比较三个函数的增长差异(以1，a，b，c，d，e为分界点)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
