
【题目】一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长![]() 与身高
与身高![]() 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为![]() )作为样本如下表所示.
)作为样本如下表所示.
脚掌长(x) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高(y) | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为![]() ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据所给数据求出回归方程,
(2)在回归方程中令![]() ,可得估计值;
,可得估计值;
(3)把4人编号后用列举法列出所有基本事件,并得出至少有1人身高在190cm以上这个事件所含基本事件,从而计算出概率.
解:(1)记样本中10人的“脚掌长”为![]() ,“身高”为
,“身高”为![]()
![]() ,
,
则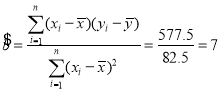 ,
,
∵![]()
![]() ,
,![]() .
.
∴![]() ,
,
∴![]() .
.
(2)由(20)知![]() ,当
,当![]() 时,
时,![]()
故估计此人的身高为![]() . .
. .
(3)将身高为181、188、197、203(cm)的4人分别记为A、B、C、D,
记“从身高180cm以上4人中随机抽取2人,所抽的2人中至少有1个身高在190cm以上”为事件A,
则基本事件有:(AB)、(AC)、(AD)、(BC)、(BD)、(CD),总数为6,
A包含的基本事件有:(AC)、(AD)、(BC)、(BD)、(CD),个数为5,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.命题“若![]() ,则
,则![]() ”的逆命题为真命题
”的逆命题为真命题
B.若![]() 为假命题,则
为假命题,则![]() 均为假命题
均为假命题
C.若![]() 为假命题,则
为假命题,则![]() 为真命题
为真命题
D.命题“若两个平面向量![]() 满足
满足![]() ,则
,则![]() 不共线”的否命题是真命题.
不共线”的否命题是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为
中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)求直线l的直角坐标方程及曲线C的普通方程;
(2)证明:直线l和曲线C相交,并求相交弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,第四日行二十四,几朝才得到其关,请公仔细算相还.”其大意为:“有一个人要走378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,其中第四天走了24里.”问此人( )天后到达目的地.
A.4B.5C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,且![]() ,平面PCD⊥平面ABCD,
,平面PCD⊥平面ABCD,![]() ,点E为线段PC的中点,点F是线段AB上的一个动点.
,点E为线段PC的中点,点F是线段AB上的一个动点.
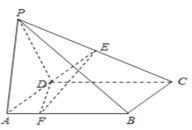
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段AB上是否存在这样的点F,使得
,试判断在线段AB上是否存在这样的点F,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P到图形C上每一个点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C的距离与到定点![]() 的距离相等的点的轨迹可能是( )
的距离相等的点的轨迹可能是( )
A.圆B.直线C.椭圆D.双曲线的一支
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等比数列,
为等比数列,![]() 公比为
公比为![]()
![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() 求
求![]()
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() 使得对任意正整数
使得对任意正整数![]() 不等式
不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com