
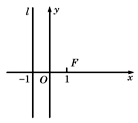
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作l的垂线,垂足为点Q,且
![]() ·
·![]()
(I)求动点P的轨迹C的方程;
(II)过点F的直线交轨迹C于A、B两点,交直线l于点M.
(1)已知![]() 的值;
的值;
(2)求|![]() |·|
|·|![]() |的最小值.
|的最小值.
0,16
解法一:(I)设点P(x,y),则Q(-1,y),由![]() 得:
得:
(x+1,0)·(2,-y)=(x-1,y)·(-2,y),化简得C:y2=4x.
(II)(1)设直线AB的方程为:
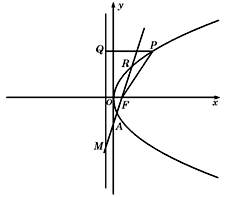
x=my+1(m≠0).
设A(x1,y1),B(x2,y2),又M(-1,-![]() ).
).
联立方程组![]() ,消去x得:
,消去x得:
y2-4my-4=0,
=(-4m)2+12>0,
![]()
由![]() 得:
得:
![]() ,整理得:
,整理得:
![]() ,
,
∴![]()
=![]()
=-2-![]()
=0.
解法二:(I)由![]()
∴![]() ·
·![]() ,
,
∴![]() =0,
=0,
∴![]()
所以点P的轨迹C是抛物线,由题意,轨迹C的方程为:y2=4x.
(II)(1)由已知![]()
则: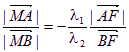 …………①
…………①
过点A、B分别作准l的垂线,垂足分别为A1、B1,
则有: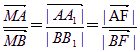 …………②
…………②
由①②得: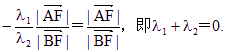
(II)(2)解:由解法一:
![]() ·
·![]() =(
=(![]() )2|y1-yM||y2-yM|
)2|y1-yM||y2-yM|
=(1+m2)|y1y2-yM(y1+y2)|+yM2|
=(1+m2)|-4+![]() ×4m+
×4m+![]() |
|
=![]()
=4(2+m2+![]() )
) ![]() 4(2+2
4(2+2![]() )=16.
)=16.
当且仅当![]() ,即m=
,即m=![]() 1时等号成立,所以
1时等号成立,所以![]() ·
·![]()
![]() 最小值为16.
最小值为16.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
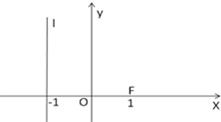 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且 |
| OP |
 |
| QF |
 |
| FP |
 |
| FQ |
 |
| MA |
 |
| AF |
 |
| MB |
 |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若| QP |
| QF |
| FP |
| FQ |
| |MA| |
| |MB| |
| |RA| |
| |RB| |
查看答案和解析>>
科目:高中数学 来源: 题型:
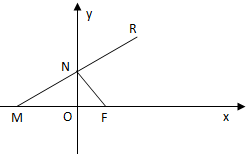 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且| NM |
| NF |
| NM |
| NR |
| 0 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且| NM |
| NF |
| NM |
| NR |
| 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年福建卷文)(本小题满分14分)
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作l的垂线,垂足为点Q,且
![]() ?
?![]()
(I)求动点P的轨迹C的方程;
(II)过点F的直线交轨迹C于A、B两点,交直线l于点M.
(1)已知![]() 的值;
的值;
(2)求|![]() |?|
|?|![]() |的最小值.
|的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com