分析:(1)用坐标表示向量,再利用向量的数量积公式,结合配方法,即可求
•的范围;
(2)分类讨论,利用
⊥,结合韦达定理,求出直线的斜率,即可求直线l的方程.
解答:解:(1)∵椭圆
+y2=1,
∴
a=,b=1,c=1,
∴F
1(-1,0),…(1分)
设A(x
1,y
1),则
•=+x1+…(3分)
∵
+y12=1,
∴
•=+x1+=+x1+1=(x1+1)2+…(5分)
∵
x1∈[-,],
∴
•∈[,+2],…(6分)
(2)设A、B两点的坐标为A(x
1,y
1)、B(x
2,y
2)
①当l平行于y轴时,点
A(-1,)、
B(-1,-),此时
•=≠0…(8分)
②当l不平行于y轴时,设直线l的斜率为k,则直线l方程为y=k(x+1),
由
得(1+2k
2)x
2+4k
2x+2k
2-2=0…(9分)
∴
x1+x2=-,
x1x2=…(11分)
∴
•=x1x2+y1y2=(1+k2)x1x2+k2(x1+x2)+k2=
(1+k2)•-k2•+k2=0解得k
2=2,
∴
k=±…(13分)
故所求的直线方程为
y=±(x+1)…(14分)
点评:本题考查椭圆方程及其性质,考查向量知识的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

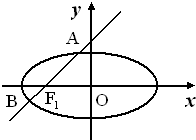 过椭圆
过椭圆

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案