Question

【题目】如图，在平面直角坐标系xOy中，椭圆C： (a＞b＞0)的离心率为，且过点(1， )．过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x＝m(m＞a)于点M．已知点B(1，0)，直线PB交l于点N．

（Ⅰ）求椭圆C的方程；

（Ⅱ）若MB是线段PN的垂直平分线，求实数m的值．

Answer 1

【答案】（1）＋y2＝1（2）m＝

【解析】试题分析：（1）根据题意列出关于 、 、的方程组，结合性质 ， ，求出 、 、，即可得结果；（2）设，则,所以．可得直线的方程为，根据可得，解方程即可得结果.

试题解析：解：（1）因为椭圆C的离心率为，所以a2＝4b2． 又因为椭圆C过点(1， )，所以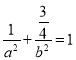 解得a2＝4，b2＝1．

所以椭圆C的方程为＋y2＝1

（2）解法1

设P(x0，y0)，－2＜x0＜2， x0≠1，则＋y02＝1．

因为MB是PN的垂直平分线，所以P关于B的对称点N(2－x0，－y0)，

所以2－x0＝m．

由A(－2，0)，P(x0，y0)，可得直线AP的方程为y＝ (x＋2)，

令x＝m，得y＝，即M(m， )．

因为PB⊥MB，所以kPB·kMB＝－1，

所以kPB·kMB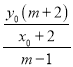＝ ＝－1，

因为＋y02＝1．所以＝1．

因为x0＝2－m ，所以化简得3m2－10m＋4＝0，

解得m＝．

因为m＞2，所以m＝．

解法2

①当AP的斜率不存在或为0时，不满足条件．

②设AP斜率为k，则AP：y＝k(x＋2)，

联立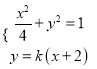消去y得(4k2＋1)x2＋16k2x＋16k2－4＝0．

因为xA＝－2，所以xP＝，所以yP＝，

所以P(， )．

因为PN的中点为B，所以m＝2－＝ (*)

因为AP交直线l于点M，所以M(m，k(m＋2))，

因为直线PB与x轴不垂直，所以≠1，即k2≠，

所以kP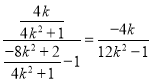B＝，kMB＝．

因为PB⊥MB，所以kPB·kMB＝－1，

所以·＝－1．（**）

将(*)代入（**），化简得48k4－32k2＋1＝0，

解得k2＝，所以m＝＝．

又因为m＞2，所以m＝．