
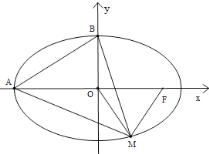
ΓΨΧβΡΩΓΩM «Ά÷‘≤TΘΚ![]() 1Θ®aΘΨbΘΨ0Θ©…œ»Έ“β“ΜΒψΘ§F «Ά÷‘≤TΒΡ”“ΫΙΒψΘ§AΈΣΉσΕΞΒψΘ§BΈΣ…œΕΞΒψΘ§OΈΣΉχ±ξ‘≠ΒψΘ§»γœ¬ΆΦΥυ ΨΘ§“―÷Σ|MF|ΒΡΉν¥σ÷ΒΈΣ3
1Θ®aΘΨbΘΨ0Θ©…œ»Έ“β“ΜΒψΘ§F «Ά÷‘≤TΒΡ”“ΫΙΒψΘ§AΈΣΉσΕΞΒψΘ§BΈΣ…œΕΞΒψΘ§OΈΣΉχ±ξ‘≠ΒψΘ§»γœ¬ΆΦΥυ ΨΘ§“―÷Σ|MF|ΒΡΉν¥σ÷ΒΈΣ3![]() Θ§«“ΓςMAFΟφΜΐΉν¥σ÷ΒΈΣ3
Θ§«“ΓςMAFΟφΜΐΉν¥σ÷ΒΈΣ3![]() Θ°
Θ°
Θ®1Θ©«σΆ÷‘≤TΒΡ±ξΉΦΖΫ≥Χ
Θ®2Θ©«σΓςABMΒΡΟφΜΐΒΡΉν¥σ÷ΒS0Θ°»τΒψNΘ®xΘ§yΘ©¬ζΉψxΓ ZΘ§yΓ ZΘ§≥ΤΒψNΈΣΗώΒψΘ°Έ Ά÷‘≤TΡΎ≤Ω «Ζώ¥φ‘ΎΗώΒψGΘ§ ΙΒΟΓςABGΒΡΟφΜΐSΓ Θ®6Θ§S0Θ©ΘΩ»τ¥φ‘ΎΘ§«σ≥ωGΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1)![]() (2)¥φ‘ΎΘ§Ήχ±ξΈΣΘ®2Θ§©¹1Θ©
(2)¥φ‘ΎΘ§Ήχ±ξΈΣΘ®2Θ§©¹1Θ©
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Ά÷‘≤–‘÷ Ω…÷Σ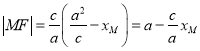 Θ§”…“―÷ΣΧθΦΰΒΟ
Θ§”…“―÷ΣΧθΦΰΒΟ![]() Θ§«“
Θ§«“![]() ΒΡΉν¥σ÷ΒΈΣ2Θ§Φ¥b=2Θ§ΫαΚœaΘ§bΘ§cΒΡΙΊœΒΩ…«σ≥ωΆ÷‘≤TΒΡΖΫ≥ΧΘ°
ΒΡΉν¥σ÷ΒΈΣ2Θ§Φ¥b=2Θ§ΫαΚœaΘ§bΘ§cΒΡΙΊœΒΩ…«σ≥ωΆ÷‘≤TΒΡΖΫ≥ΧΘ°
Θ®2Θ©”…Χβ÷Σ÷±œΏABΒΡΖΫ≥ΧΈΣ![]() Θ§…η÷±œΏ
Θ§…η÷±œΏ![]() ”κΆ÷‘≤Tœύ«–”Ύx÷αœ¬ΖΫΒΡΒψM0Θ§‘ρΓςABM0ΒΡΟφΜΐΈΣΓςABMΒΡΟφΜΐΒΡΉν¥σ÷ΒS0Θ°÷±œΏ”κΆ÷‘≤ΝΣΝΔ«σ≥ω÷±œΏAB”κ÷±œΏlΨύάκΈΣ
”κΆ÷‘≤Tœύ«–”Ύx÷αœ¬ΖΫΒΡΒψM0Θ§‘ρΓςABM0ΒΡΟφΜΐΈΣΓςABMΒΡΟφΜΐΒΡΉν¥σ÷ΒS0Θ°÷±œΏ”κΆ÷‘≤ΝΣΝΔ«σ≥ω÷±œΏAB”κ÷±œΏlΨύάκΈΣ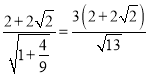 Θ§”…¥ΥΡή«σ≥ωΘ®2Θ§©¹1Θ©ΈΣΥυ«σΗώΒψGΘ°
Θ§”…¥ΥΡή«σ≥ωΘ®2Θ§©¹1Θ©ΈΣΥυ«σΗώΒψGΘ°
Θ®1Θ©”…Ά÷‘≤–‘÷ Ω…÷Σ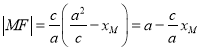 Θ§
Θ§
Τδ÷–cΘΨ0Θ§c2ΘΫa2©¹b2Θ§
“ρΈΣxMΓ [©¹aΘ§a]Θ§Ι |MF|Γ [a©¹cΘ§a+c]Θ§Φ¥![]()
”÷ΓςMAFΟφΜΐΉν¥σ÷ΒΈΣ3![]() Θ°«“
Θ°«“ ![]() Θ§Γύ
Θ§Γύ![]() ΒΡΉν¥σ÷ΒΈΣ2Θ§Φ¥b=2Θ§”÷b2ΘΫa2©¹c2«“
ΒΡΉν¥σ÷ΒΈΣ2Θ§Φ¥b=2Θ§”÷b2ΘΫa2©¹c2«“![]()
Ϋβ÷°ΒΟ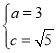
Ά÷‘≤TΒΡΖΫ≥ΧΈΣ![]()
Θ®2Θ©”…Χβ÷Σ÷±œΏABΒΡΖΫ≥ΧΈΣ![]() Θ§
Θ§
…η÷±œΏ![]() ”κΆ÷‘≤Tœύ«–”Ύx÷αœ¬ΖΫΒΡΒψM0Θ§
”κΆ÷‘≤Tœύ«–”Ύx÷αœ¬ΖΫΒΡΒψM0Θ§
‘ρΓςABM0ΒΡΟφΜΐΈΣΓςABMΒΡΟφΜΐΒΡΉν¥σ÷ΒS0.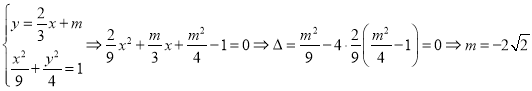
¥Υ ±Θ§÷±œΏAB”κ÷±œΏlΨύάκΈΣ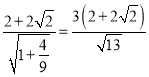 Θ§
Θ§
Εχ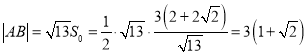
Εχ![]() Θ§Νν
Θ§Νν![]() Θ§‘ρ
Θ§‘ρ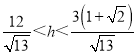
…η÷±œΏ![]() ΒΫ÷±œΏABΒΡΨύάκΈΣ
ΒΫ÷±œΏABΒΡΨύάκΈΣ![]() Θ§
Θ§
‘ρ”–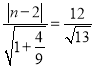 Θ§ΫβΒΟnΘΫ©¹2Μρ6Θ§
Θ§ΫβΒΟnΘΫ©¹2Μρ6Θ§
ΉΔ“βΒΫl1”κ÷±œΏABΤΫ––«“l1–η”κΆ÷‘≤T”Π”–ΙΪΙ≤ΒψΘ§
Ι ÷Μ–ηΩΦ¬«nΘΫ©¹2ΒΡ«ι–ΈΘ°
÷±œΏ![]() Ψ≠ΙΐΆ÷‘≤TΒΡœ¬ΕΞΒψB0Θ®0Θ§©¹2Θ©”κ”“ΕΞΒψA0Θ§
Ψ≠ΙΐΆ÷‘≤TΒΡœ¬ΕΞΒψB0Θ®0Θ§©¹2Θ©”κ”“ΕΞΒψA0Θ§
‘ρœΏΕΈA0B0…œ»Έ“β“ΜΒψG0”κAΓΔBΉι≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ6
ΗυΨίΧβ“β»τ¥φ‘Ύ¬ζΉψΧβ“βΒΡΗώΒψGΘ§‘ρG±Ί‘Ύ÷±œΏA0B0”κl÷°ΦδΘ°
Εχ‘ΎΆ÷‘≤ΡΎ≤ΩΈΜ”ΎΥΡœσœόΒΡΗώΒψΈΣΘ®1Θ§©¹1Θ©Θ§Θ®2Θ§©¹1Θ©
“ρΈΣ![]() Θ§Ι Θ®1Θ§©¹1Θ©‘Ύ÷±œΏA0B0…œΖΫΘ§≤ΜΖϊΧβ“β
Θ§Ι Θ®1Θ§©¹1Θ©‘Ύ÷±œΏA0B0…œΖΫΘ§≤ΜΖϊΧβ“β
Εχ![]() Θ§‘ρΒψΘ®2Θ§©¹1Θ©‘Ύ÷±œΏA0B0œ¬ΖΫΘ§
Θ§‘ρΒψΘ®2Θ§©¹1Θ©‘Ύ÷±œΏA0B0œ¬ΖΫΘ§
«“![]() Θ§Βψ‘ΎΆ÷‘≤ΡΎ≤ΩΘ§
Θ§Βψ‘ΎΆ÷‘≤ΡΎ≤ΩΘ§
Υυ“‘Θ®2Θ§©¹1Θ©ΈΣΥυ«σΗώΒψGΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©»τ![]() ‘ΎΕ®“ε”ρΡΎ”–ΝΫΗωΦΪ÷ΒΒψ
‘ΎΕ®“ε”ρΡΎ”–ΝΫΗωΦΪ÷ΒΒψ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Ε·Βψ
÷–Θ§Ε·Βψ![]() ”κΝΫΕ®Βψ
”κΝΫΕ®Βψ![]() Ν§œΏΒΡ–±¬ ÷°ΜΐΈΣ
Ν§œΏΒΡ–±¬ ÷°ΜΐΈΣ![]() Θ§Φ«Βψ
Θ§Φ«Βψ![]() ΒΡΙλΦΘΈΣ«ζœΏ
ΒΡΙλΦΘΈΣ«ζœΏ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©»τΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§«ζœΏ
ΝΫΒψΘ§«ζœΏ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ![]() ΙΒΟΥΡ±Ώ–Έ
ΙΒΟΥΡ±Ώ–Έ![]() ΈΣΤΫ––ΥΡ±Ώ–ΈΘΩ»τ¥φ‘ΎΘ§«σ÷±œΏ
ΈΣΤΫ––ΥΡ±Ώ–ΈΘΩ»τ¥φ‘ΎΘ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”….
ΒΡΖΫ≥ΧΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψH‘Ύ’ΐΖΫΧε![]() ΒΡΕ‘Ϋ«œΏ
ΒΡΕ‘Ϋ«œΏ![]() …œΘ§ΓœHDA=
…œΘ§ΓœHDA=![]() Θ°
Θ°

Θ®1Θ©«σDH”κ![]() Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σDH”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΕ“ΉΨ≠ΓΖ «÷–Ιζ¥ΪΆ≥ΈΡΜ·÷–ΒΡΨΪΥηΘ§»γΆΦ «“ΉΨ≠ΑΥΊ‘Θ®Κ§«§ΓΔάΛΓΔΌψΓΔ’πΓΔΩ≤ΓΔάκΓΔτόΓΔΕ“ΑΥΊ‘Θ©Θ§ΟΩ“ΜΊ‘”…»ΐΗυœΏΉι≥…Θ®"![]() "±μ Ψ“ΜΗυ―τœΏΘ§"
"±μ Ψ“ΜΗυ―τœΏΘ§"![]() "±μ Ψ“ΜΗυ“θœΏΘ©Θ§¥”ΑΥΊ‘÷–»Έ»ΓΝΫΊ‘Θ§’βΝΫΊ‘ΒΡΝυΗυœΏ÷–«Γ”–ΝΫΗυ―τœΏΘ§ΥΡΗυ“θœΏΒΡΗ≈¬ ΈΣ_______.
"±μ Ψ“ΜΗυ“θœΏΘ©Θ§¥”ΑΥΊ‘÷–»Έ»ΓΝΫΊ‘Θ§’βΝΫΊ‘ΒΡΝυΗυœΏ÷–«Γ”–ΝΫΗυ―τœΏΘ§ΥΡΗυ“θœΏΒΡΗ≈¬ ΈΣ_______.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈADEF”κΧί–ΈABCDΥυ‘ΎΒΡΤΫΟφΜΞœύ¥Ι÷±Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
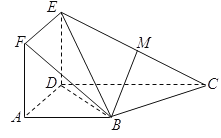
Θ®1Θ©«σ÷ΛΘΚBMΓΈΤΫΟφADEFΘΜ
Θ®2Θ©«σ÷ΛΘΚΤΫΟφBDEΓΆΤΫΟφBECΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΐ‘≠ΒψΒΡΕ·÷±œΏl”κ‘≤![]() œύΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ°
œύΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ°
Θ®1Θ©«σœΏΕΈABΒΡ÷–ΒψMΒΡΙλΦΘCΒΡΖΫ≥ΧΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐkΘ§ ΙΒΟ÷±œΏLΘΚy=kΘ®x©¹4Θ©”κ«ζœΏC÷Μ”–“ΜΗωΫΜΒψΘΩ»τ¥φ‘ΎΘ§«σ≥ωkΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ»≤ν ΐΝ–ΒΡ![]() ΙΪ≤ν
ΙΪ≤ν![]() ≤ΜΈΣ0Θ§
≤ΜΈΣ0Θ§![]() «Τδ«Α
«Τδ«Α![]() œνΚΆΘ§Ηχ≥ωœ¬Ν–ΟϋΧβΘΚ
œνΚΆΘ§Ηχ≥ωœ¬Ν–ΟϋΧβΘΚ
ΔΌ»τ![]() Θ§«“
Θ§«“![]() Θ§‘ρ
Θ§‘ρ![]() ΚΆ
ΚΆ![]() ΕΦ «
ΕΦ «![]() ÷–ΒΡΉν¥σœνΘΜ
÷–ΒΡΉν¥σœνΘΜ
ΔΎΗχΕ®![]() Θ§Ε‘“Μ«–
Θ§Ε‘“Μ«–![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() ΘΜ
ΘΜ
Δέ»τ![]() Θ§‘ρ
Θ§‘ρ![]() ÷–“ΜΕ®”–Ήν–ΓœνΘΜ
÷–“ΜΕ®”–Ήν–ΓœνΘΜ
Δή¥φ‘Ύ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΚΆ
ΚΆ![]() Ά§Κ≈.
Ά§Κ≈.
Τδ÷–’ΐ»ΖΟϋΧβΒΡΗω ΐΈΣΘ® Θ©
A.4B.3C.2D.1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΧαΗΏ≥« –Ψ”Οώ…ζΜν–“ΗΘΗ–Θ§Ρ≥≥« –ΙΪΫΜΙΪΥΨ¥σΝΠ»Ζ±ΘΙΪΫΜ≥ΒΒΡΉΦΒψ¬ Θ§Φθ…ΌΨ”Οώ≥Υ≥ΒΚρ≥Β ±ΦδΈΣ¥ΥΘ§ΗΟΙΪΥΨΕ‘Ρ≥’ΨΧ®≥ΥΩΆΒΡΚρ≥Β ±ΦδΫχ––Ά≥ΦΤ≥ΥΩΆΚρ≥Β ±Φδ ήΙΪΫΜ≥ΒΉΦΒψ¬ ΓΔΫΜΆ®”ΒΕ¬«ιΩωΓΔΫΎΦΌ»’»ΥΝςΝΩ‘ω¥σΒ»«ιΩω”Αœλ‘ΎΙΪΫΜ≥ΒΉΦΒψ¬ ’ΐ≥ΘΓΔΫΜΆ®”ΒΕ¬«ιΩω’ΐ≥ΘΓΔΖ«ΫΎΦΌ»’ΒΡ«ιΩωœ¬Θ§≥ΥΩΆΚρ≥Β ±ΦδΥφΜζ±δΝΩ![]() ¬ζΉψ’ΐΧ§Ζ÷≤Φ
¬ζΉψ’ΐΧ§Ζ÷≤Φ![]() ‘ΎΙΪΫΜ≥ΒΉΦΒψ¬ ’ΐ≥ΘΓΔΫΜΆ®”ΒΕ¬«ιΩω’ΐ≥ΘΓΔΖ«ΫΎΦΌ»’ΒΡ«ιΩωœ¬Θ§Βς≤ιΝΥ¥σΝΩ≥ΥΩΆΒΡΚρ≥Β ±ΦδΘ§Ψ≠ΙΐΆ≥ΦΤΒΟΒΫ»γΆΦΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
‘ΎΙΪΫΜ≥ΒΉΦΒψ¬ ’ΐ≥ΘΓΔΫΜΆ®”ΒΕ¬«ιΩω’ΐ≥ΘΓΔΖ«ΫΎΦΌ»’ΒΡ«ιΩωœ¬Θ§Βς≤ιΝΥ¥σΝΩ≥ΥΩΆΒΡΚρ≥Β ±ΦδΘ§Ψ≠ΙΐΆ≥ΦΤΒΟΒΫ»γΆΦΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
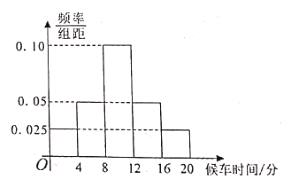
Θ®1Θ©‘Ύ÷±ΖΫΆΦΗςΉι÷–Θ§“‘ΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζ±μΗΟΉι÷–ΒΡΗςΗω÷ΒΘ§ ‘ΙάΦΤ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©‘ΎΆ≥ΦΤ―ß÷–Θ§ΖΔ…ζΗ≈¬ ΒΆ”Ύ«ßΖ÷÷°»ΐΒΡ ¬ΦΰΫ––ΓΗ≈¬ ¬ΦΰΘ§“ΜΑψ»œΈΣΘ§‘Ύ’ΐ≥Θ«ιΩωœ¬Θ§“Μ¥Έ ‘―ι÷–Θ§–ΓΗ≈¬ ¬Φΰ «≤ΜΡήΖΔ…ζΒΡ‘ΎΫΜΆ®”ΒΕ¬«ιΩω’ΐ≥ΘΓΔΖ«ΫΎΦΌ»’ΒΡΡ≥ΧλΘ§ΥφΜζΒς≤ιΝΥΗΟ’ΨΒΡ10Οϊ≥ΥΩΆΒΡΚρ≥Β ±ΦδΘ§ΖΔœ÷Τδ÷–”–3Οϊ≥ΥΩΆΚρ≥Β ±Φδ≥§Ιΐ15Ζ÷÷”Θ§ ‘≈–ΕœΗΟΧλΙΪΫΜ≥ΒΉΦΒψ¬ «Ζώ’ΐ≥ΘΘ§ΥΒΟςάμ”….
Θ®≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com