
已知椭圆![]() ,直线l:
,直线l:![]() ,P点是l上一点,射线OP交椭圆于点R,又点Q在OP上且满足
,P点是l上一点,射线OP交椭圆于点R,又点Q在OP上且满足![]() 。当点P在l上移动时,求点Q的轨迹方程。
。当点P在l上移动时,求点Q的轨迹方程。
解法一:设Q![]() ,Q点不在原点,
,Q点不在原点,![]()
显然x,y不同是为零
①P点不在y轴时,即![]() 时
时
∵ R不在椭圆上
∴ 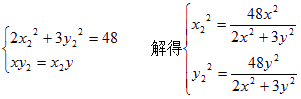
又∵ ![]()
∵ P点在直线l上,∴ 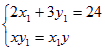
解得: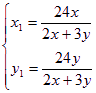
∵ ![]()
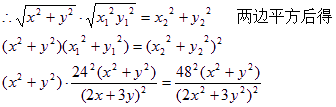
∵ x、y不同时为零
∴ ![]()
∵ Q点与坐标原点O在直线l的同侧
∴ ![]()
则:![]()
即:![]()
②P点在y轴上时,P(0,8)
k(0,4)
![]() 可得Q(0,2),Q点满足这个方程
可得Q(0,2),Q点满足这个方程
∴ 所求的轨迹方程是![]()
|
|
解法二:点的坐标同上,过P、R、Q分别作y轴的垂线,垂足分别记作![]()
∵ ![]()
又∵ ![]()
∴ ![]()
即 ![]()
由题已知 ![]() 三个量同号
三个量同号
∴ ![]()
设 射线OP方程为![]()
则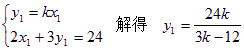
又R也在OP上,∴ 
代入![]() 中
中
![]()
![]()
化简: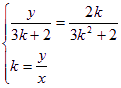

∵ ![]()
则![]() 为所求的轨迹方程
为所求的轨迹方程
本题动点Q的运动依赖于①P点的运动。②![]() 这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤
这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤ ![]() 中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将
中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将![]() 转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l:
转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l:![]() 上运动,而该直线与y轴可以相交,当P点在 y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
上运动,而该直线与y轴可以相交,当P点在 y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
综上,在圆锥曲线的标准方程这部分内容中,应掌握的求曲线方程的基本方法。由于求曲线方程是平面解析几何两个主要内容之一,可以题型多,方法多。但因为坐标轴平移还没学到因而涉及到园锥曲线的一般式的问题后再讲。


科目:高中数学 来源:2014届湖北孝感高级中学高二上学期期末考试理科数学试卷(解析版) 题型:解答题
已知椭圆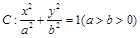 ,直线l为圆
,直线l为圆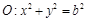 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为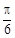 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.
(1)求e的值;
(2)试判定原点关于l的对称点是否在椭圆上,并说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三压轴文科数学试卷(解析版) 题型:解答题
(本小题共13分)
已知椭圆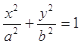
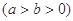 和直线L:
和直线L: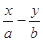 =1, 椭圆的离心率
=1, 椭圆的离心率 ,直线L与坐标原点的距离为
,直线L与坐标原点的距离为 。
。
(1)求椭圆的方程;
(2)已知定点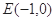 ,若直线
,若直线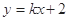
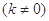 与椭圆相交于C、D两点,试判断是否存在
与椭圆相交于C、D两点,试判断是否存在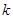 值,使以CD为直径的圆过定点E?若存在求出这个
值,使以CD为直径的圆过定点E?若存在求出这个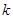 值,若不存在说明理由。
值,若不存在说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三上学期期末考试数学理卷 题型:解答题
(12分)已知椭圆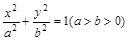 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且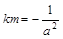 .
.

(Ⅰ)求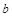 的值;
的值;
(Ⅱ)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈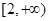 ,使得四边形OACB是平行四边形,请证明你的结论;
,使得四边形OACB是平行四边形,请证明你的结论;
查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省泉州市南安一中高二(上)年期末数学试卷(文科)(解析版) 题型:解答题
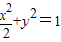 及直线l:y=x+m.
及直线l:y=x+m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com