
在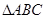 中,
中, 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长, ,
,
 .
.
(1)求角B的大小。
(2)若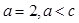 求
求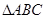 的面积
的面积 .
.
(1)角B为 ;(2)
;(2) .
.
【解析】
试题分析:本题考查解三角形中的正弦定理的运用以及运用三角公式进行三角变换的能力和三角形面积公式,考查基本的运算能力.第一问,由正弦定理得 ,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得
,再利用两角和与差的正弦公式和倍角公式化简第二个已知条件,两式结合,得 ,注意是在三角形中求角
,注意是在三角形中求角 ;第二问,结合第一问的结论,得
;第二问,结合第一问的结论,得 ,通过边的大小确定角
,通过边的大小确定角 的大小,已知有
的大小,已知有 边的长度,要求三角形面积还需求
边的长度,要求三角形面积还需求 角,由
角,由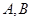 角求
角求 角,从而求出
角,从而求出 ,所以代入三角形面积公式中即可.
,所以代入三角形面积公式中即可.
试题解析:(1)由正弦定理及已知可得 1分
1分
 得
得 4分
4分
所以 解得
解得 又因为在
又因为在 ABC中
ABC中
所以角B为 6
6 分
分
(2)由(1)知 又因为
又因为 所以
所以 7分
7分
所以

 9分
9分
 12分
12分
考点:1.正弦定理;2.两角和与差的正弦公式;3.三角形面积公式.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2011年广东省揭阳市高二上学期期末检测数学理卷 题型:解答题
若(本题12分)在△ABC中,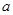 ,
,  ,
,  分别为内角A, B, C的对边,且
分别为内角A, B, C的对边,且

(Ⅰ)求A的大小; (Ⅱ)求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com