
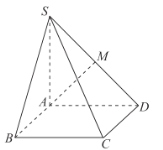
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 是边长为
是边长为![]() 的正方形.且
的正方形.且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明出![]() 平面
平面![]() ,由直线与平面垂直的定义可得出
,由直线与平面垂直的定义可得出![]() ;
;
(2)解法一:以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,由题意得出平面
,由题意得出平面![]() 与平面
与平面![]() 的一个法向量分别为
的一个法向量分别为![]() 、
、![]() ,然后利用空间向量法计算出平面
,然后利用空间向量法计算出平面![]() 与平面
与平面![]() 所成的锐二面角;
所成的锐二面角;
解法二:过![]() 引直线
引直线![]() ,使得
,使得![]() ,可知
,可知![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的棱,并证明出
所成二面角的棱,并证明出![]() ,
,![]() ,由二面角的定义得出
,由二面角的定义得出![]() 为平面
为平面![]() 与平面
与平面![]() 所成的锐二面角,然后在
所成的锐二面角,然后在![]() 计算出该角即可.
计算出该角即可.
(1)由题意,底面![]() 是正方形,
是正方形,![]() .
.
![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
又![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() ;
;
(2)法—:由题知![]() 、
、![]() 、
、![]() 两两垂直,以
两两垂直,以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.

则![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() 平面
平面![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() ,
,
由(1)知![]() 平面
平面![]() ,
,![]() 是平面
是平面![]() 的一个法向量,且
的一个法向量,且![]() ,
,
∴ ,
,
因此,平面![]() 与平面
与平面![]() 所成锐二面角的大小等于
所成锐二面角的大小等于![]() ;
;
法二:过![]() 引直线
引直线![]() ,使得
,使得![]() ,则
,则![]() ,
,

![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角的棱.
所成二面角的棱.
由条件知,![]() ,
,![]() ,已知
,已知![]() ,则
,则![]() 平面
平面![]() .
.
由作法知![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,
![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成锐二面角的平面角.
所成锐二面角的平面角.
在![]() 中,
中,![]() ,
,![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的大小等于
所成锐二面角的大小等于![]() .
.


科目:高中数学 来源: 题型:
【题目】某市旅游局为了进一步开发旅游资源,需要了解游客的情况,以便制定相应的策略,在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下:若景点甲中的数据的中位数是126,景点乙中的数据的平均数是124.
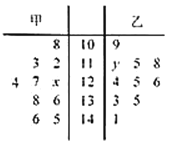
(1)求![]() ,
,![]() 的值;
的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据(视样本频率为概率).今从这段时期内任取4天,记其中游客数不低于125人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于135人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数、众数、中位数。(不要求写过程)
(3) 从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某IT从业者绘制了他在26岁~35岁(2009年~2018年)之间各年的月平均收入(单位:千元)的散点图:

(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据附注提供的有关数据建立
的关系,试根据附注提供的有关数据建立![]() 关于
关于![]() 的回归方程
的回归方程
(2)若把月收入不低于2万元称为“高收入者”.

试利用(1)的结果,估计他36岁时能否称为“高收入者”?能否有95%的把握认为年龄与收入有关系?
附注:①.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,取
,取![]() ,
,![]()
②.参考公式:回归方程![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计分别为:
的最小二乘估计分别为: ,
,![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
③. .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题:
①若![]() ,则
,则![]() 或
或![]() 的逆命题;
的逆命题;
②若![]() ,则
,则![]() 的逆否命题;
的逆否命题;
③若![]() 、
、![]() ,
,![]() 是奇数,则
是奇数,则![]() 、
、![]() 中一个是奇数,一个是偶数.
中一个是奇数,一个是偶数.
其中真命题的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为
表示值域为![]() 的函数组成的集合,
的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() 。例如,当
。例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() 。则下列命题中正确的是:( )
。则下列命题中正确的是:( )
A.设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”
”
B.函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值
有最大值和最小值
C.若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]()
D.若函数![]() 有最大值,则
有最大值,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com