
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,由已知
,由已知![]() ,求得
,求得![]() 的坐标为
的坐标为![]() ,代入椭圆方程,得
,代入椭圆方程,得![]() ;再由
;再由![]() ,求得
,求得![]() ,结合
,结合![]() ,求出
,求出![]() 值,即可求得结论;
值,即可求得结论;
(2)先讨论直线![]() 斜率不存在和斜率为0的情况,验证不满足条件,设直线
斜率不存在和斜率为0的情况,验证不满足条件,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,消元,由韦达定理和相交弦长公式,求出
,与椭圆方程联立,消元,由韦达定理和相交弦长公式,求出![]() ;
;
再将直线![]() 方程
方程![]() 与椭圆联立,求出
与椭圆联立,求出![]() ,由
,由![]() 求出
求出![]() 的值,进而求出
的值,进而求出![]() ,再求出点
,再求出点![]() 到直线
到直线![]() 的距离,即可求解.
的距离,即可求解.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,∵
,∵![]() ,
,
∴![]() 的坐标为
的坐标为![]() .∵
.∵![]() 在
在![]() 上,
上,
将![]() 代人
代人![]() ,得
,得![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() .又∵
.又∵![]() ,
,
∴![]() ,
,![]() ,
,![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,![]() ,不符合题意;
,不符合题意;
当直线![]() 的斜率为0时,
的斜率为0时,![]() ,
,![]() ,也不符合题意.
,也不符合题意.
∴可设直线![]() 的方程为
的方程为![]() ,
,
联立 得
得![]() ,
,
则![]() ,
,![]() .
.
![]() .
.
由 得
得 或
或
∴![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .∵
.∵![]() 到直线
到直线![]() 的距离
的距离 ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
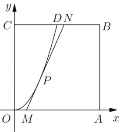
【题目】某地要建造一个边长为2(单位:![]() )的正方形市民休闲公园
)的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过边
图像的一部分,过边![]() 上一点
上一点![]() 在区域
在区域![]() 内作一次函数
内作一次函数![]() (
(![]() )的图像,与线段
)的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
(1)求证:![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 两点的坐标;
两点的坐标;
②将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对职工开展了安全知识竞赛的活动,将竞赛成绩按照![]() ,
,![]() ,… ,
,… ,![]() 分成
分成![]() 组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )
组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )
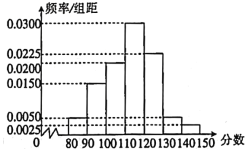
①根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的众数估计值为![]() ;
;
②根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的中位数约为![]() ;
;
③若该商场有![]() 名职工,考试成绩在
名职工,考试成绩在![]() 分以下的被解雇,则解雇的职工有
分以下的被解雇,则解雇的职工有![]() 人;
人;
④若该商场有![]() 名职工,商场规定只有安全知识竞赛超过
名职工,商场规定只有安全知识竞赛超过![]() 分(包括
分(包括![]() 分)的人员才能成为安全科成员,则安全科成员有
分)的人员才能成为安全科成员,则安全科成员有![]() 人.
人.
A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市实施二手房新政一年多以来,为了了解新政对居民的影响,房屋管理部门调查了2018年6月至2019年6月期间购买二手房情况,首先随机抽取了其中的400名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )讲行了一次统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年6月至2019年6月期间当月在售二手房的均价
)讲行了一次统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年6月至2019年6月期间当月在售二手房的均价![]() (单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年6月至2019年6月)
(单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年6月至2019年6月)
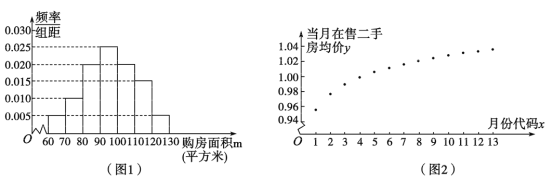
(1)试估计该市市民的平均购房面积![]() (同一组中的数据用该组区间的中点值为代表);
(同一组中的数据用该组区间的中点值为代表);
(2)从该市2018年6月至2019年6月期间所有购买二手房的市民中任取3人,用频率估计概率,记这3人购房面积不低于100平方米的人数为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)根据散点图选择![]() 和
和![]() 两个模型讲行拟合,经过数据处理得到两个回归方程,分别为
两个模型讲行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如表所示:
,并得到一些统计量的值,如表所示:
|
| |
| 0.005459 | 0.005886 |
| 0.006050 | |
请利用相关系数判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年8月份的二手房购房均价(精确到0.001).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: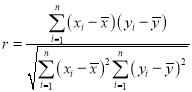
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有( )
①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人;
②用简单随机抽样的方法从新生中选出100人;
③西部地区学生小刘被选中的概率为![]() ;
;
④中部地区学生小张被选中的概率为![]()
A. ①④ B. ①③ C. ②④ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com