已知-1≤a≤1,解关于x的不等式:ax2-2x+a>0.
解:①当a=0时,原式化为-2x>0,即x<0;a≠0时,△=(-2)
2-4a
2=4(1+a)(1-a)…(1分)
②当a=-1时,△=0,原式化为-(x+1)
2>0,即 (x+1)
2<0,∴x∈∅…(2分)
③当-1<a<0时,△>0,方程ax
2-2x+a>0的根为x
1、2=
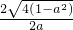
=
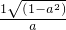
,
∴
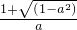
<x<
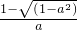
…(6分)
④当0<a<1时,结合③知,x<
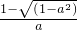
或x>
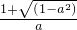
…(10分)
⑤当a=1时,原式化为x
2-2x+1>0,即(x-1)
2>0,∴x∈R,且x≠1…(11分)
总之,原不等式的解集为:当a=-1时,x∈∅;当-1<a<0时,x∈(
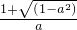
,
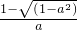
);
当a=0时,x∈(-∞,0);当0<a<1时,x∈(-∞,
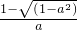
)∪(
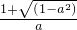
,+∞);
当a=1时,{x|x∈R,且x≠1}…(12分)
分析:针对a的值,分类讨论①当a=0时,②当a=-1时,③当-1<a<0时,④当0<a<1时,⑤当a=1时,最后综合可得.
点评:本题考查含参数的不等式的解法,熟练的分类讨论是解决问题的关键,属中档题.

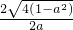 =
=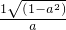 ,
,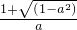 <x<
<x<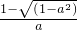 …(6分)
…(6分)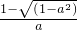 或x>
或x>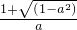 …(10分)
…(10分)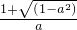 ,
,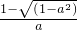 );
);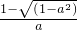 )∪(
)∪(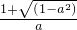 ,+∞);
,+∞);
