Question

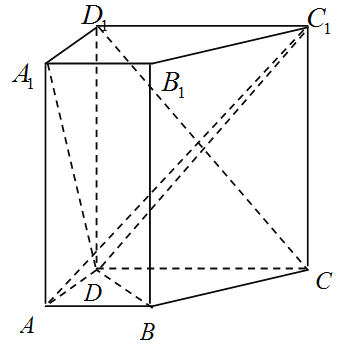
【题目】如图，在直四棱柱中，已知，．

（1）求证：；

（2）设是上一点，试确定的位置，使平面，并说明理由．

Answer 1

【答案】⑴连DC1,正方形DD1C1C中,D1C⊥C1D

∵AD⊥平面DD1C1C ∴AD⊥CD1又AD∩CD1=D

∴CD1⊥平面DA C1

⑵ E 为AC中点时，平面9’

梯形ABCD中，DE∥且=" AB " ∴AD∥且=BE

∵AD∥且= A1D1∴A1D1∥且="BE " ∴A1D1EB是平行四边形

∴D1E∥B A1又B A1平面DB A1D1E平面DB A1

∴平面

【解析】试题分析：

（1）本题为证线与线垂直，常规思路为转化为证线与另一条

直线所在的平面垂直。结合条件，可证出平面，则得：.

（2）本题为通过确定点的位置来证明证线与面平行，可通过题中的条件进行大胆设想，（为中点），然后进行对应的证明，可解决；

试题解析：

（1）在直四棱柱中，

连结，，四边形是正方形．．

又，，

平面，平面，

．平面，且，

平面，又平面，．

（2）连结，连结，设，

，连结，平面平面，

要使平面，须使，

又是的中点．是的中点．

又易知，．

即是的中点．综上所述，当是的中点时，可使平面．