
【题目】设函数![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)若对任意的实数![]() ,函数
,函数![]() (
(![]() 为实常数)的图象与函数
为实常数)的图象与函数![]() 的图象总相切于一个定点.
的图象总相切于一个定点.
① 求![]() 与
与![]() 的值;
的值;
② 对![]() 上的任意实数
上的任意实数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)0;(2)①![]() ;②
;②![]() .
.
【解析】试题分析:
(1)由奇函数的 定义得到关于实数a的方程,解方程可得a=0;
(2)由导函数研究函数的 切线可得切点为![]() ,切线的方程为
,切线的方程为![]() ,则
,则![]() .
.
(3)由题意分类讨论 ![]() 和
和![]() 两种情况可得实数
两种情况可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
解:(1)因为函数![]() 是奇函数,所以
是奇函数,所以![]() 恒成立,
恒成立,
即![]() ,得
,得![]() 恒成立,
恒成立,
![]() .
.
(2)①![]() ,设切点为
,设切点为![]() ,
,
则切线的斜率为![]() ,
,
据题意![]() 是与
是与![]() 无关的常数,故
无关的常数,故![]() ,切点为
,切点为![]() , 由点斜式得切线的方程为
, 由点斜式得切线的方程为![]() ,即
,即![]() ,故
,故![]() .
.
② 当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ;
;
当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ;
;
故![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立.
恒成立.
而![]() ,设函数
,设函数![]() .
.
则![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立,
恒成立, ![]() ,
,
![]() 当
当![]() 时,
时, ![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上递增,
上递增, ![]() ,
,
故![]() 在
在![]() 上恒成立,符合题意.
上恒成立,符合题意. ![]() 当
当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 在
在![]() 上递减,所以
上递减,所以![]() ,
,
而![]() 设函数
设函数![]() ,
,
则![]() ,
, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上递增,
上递增, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上递增,
上递增, ![]() 恒成立,
恒成立,
即![]() ,而
,而![]() ,不合题意.
,不合题意.
综上![]() ,知实数
,知实数![]() 的取值范围
的取值范围![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)在平面直角坐标系xOy中,已知两点![]() 和
和![]() ,动点M满足
,动点M满足![]() ,设点M的轨迹为C,半抛物线
,设点M的轨迹为C,半抛物线![]() :
:![]() (
(![]() ),设点
),设点![]() .
.
(Ⅰ)求C的轨迹方程;
(Ⅱ)设点T是曲线![]() 上一点,曲线
上一点,曲线![]() 在点T处的切线与曲线C相交于点A和点B,求△ABD的面积的最大值及点T的坐标.
在点T处的切线与曲线C相交于点A和点B,求△ABD的面积的最大值及点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
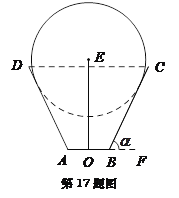
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆Cx2+y2+2x﹣4y+3=0
(1)已知不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)求经过原点且被圆C截得的线段长为2的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.交易会开始前,展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系,查阅了最近5次交易会的参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下数据:
(袋),得到如下数据:

(Ⅰ)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() 投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
(参考公式: 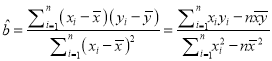 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com