
【题目】对于函数![]() ,若存在正实数
,若存在正实数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上是有界函数,下列函数:
上是有界函数,下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
其中在![]() 上是有界函数的序号为________.
上是有界函数的序号为________.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】给出下列三个命题:
①若![]() ,则
,则![]() 或
或![]() 的逆命题;
的逆命题;
②若![]() ,则
,则![]() 的逆否命题;
的逆否命题;
③若![]() 、
、![]() ,
,![]() 是奇数,则
是奇数,则![]() 、
、![]() 中一个是奇数,一个是偶数.
中一个是奇数,一个是偶数.
其中真命题的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知椭圆![]() ,
,![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,且
,且![]() ,
,![]() .
.

(Ⅰ)求椭圆的方程:
(Ⅱ)设![]() 为椭圆上异于
为椭圆上异于![]() 且不重合的两点,且
且不重合的两点,且![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴,是否存在实数
轴,是否存在实数![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() 的最大值,若不存在,请说明理由.
的最大值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水域受到污染,水务部门决定往水中投放一种药剂来净化水质,已知每次投放质量为![]() 的药剂后,经过
的药剂后,经过![]() (
(![]() )天,该药剂在水中释放的浓度
)天,该药剂在水中释放的浓度![]() (毫克
(毫克![]() 升)为
升)为![]() ,其中
,其中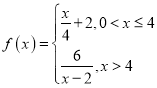 ,当药剂在水中释放浓度不低于
,当药剂在水中释放浓度不低于![]() (毫克
(毫克![]() 升)时称为有效净化,当药剂在水中释放的浓度不低于
升)时称为有效净化,当药剂在水中释放的浓度不低于![]() (毫克
(毫克![]() 升)且不高于
升)且不高于![]() (毫克
(毫克![]() 升)时称为最佳净化.
升)时称为最佳净化.
(1)如果投放的药剂质量为![]() ,那么该水域达到有效净化一共可持续几天?
,那么该水域达到有效净化一共可持续几天?
(2)如果投放的药剂质量为![]() ,为了使该水域
,为了使该水域![]() 天(从投放药剂算起,包括第
天(从投放药剂算起,包括第![]() 天)之内都达到最佳净化,确定应该投放的药剂质量
天)之内都达到最佳净化,确定应该投放的药剂质量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售量8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某微信群主发60个随机红包(即每个人抢到的红包中的钱数是随机的,且每人只能抢一个),红包被一抢而空,后据统计,60个红包中的钱数(单位:元)分配如下频率分布直方图所示(其分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).

(1)求频率分布直方图中![]() 的值及红包钱数的平均值;
的值及红包钱数的平均值;
(2)试估计该群中某成员抢到钱数不小于3元的概率;
(3)若该群中成员甲、乙两人都抢到4.5元红包,现系统将从抢到4元及以上红包的人中随机抽取2人,求甲、乙至少有一人被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com