[题目]已知:tan(α+ )=﹣ .( ＜α＜π)．(1)求tanα的值,(2)求的值．题目和参考答案——青夏教育精英家教网—

【题目】已知：tan（α+ ）=﹣ ，（＜α＜π）．
（1）求tanα的值；
（2）求的值．

【答案】
（1）解：∵tan（α+ ）= =﹣ ，（＜α＜π），∴tanα=﹣5．
（2）解：∵tanα=﹣5= ，∴α为钝角，∴sinα＞0，cosα＜0，

再结合sin2α+cos2α=1，可得cosα=﹣ ，

∴ = =2 cosα=﹣

【解析】（1）直接利用同角三角函数的基本关系、两角和的正切公式求得tanα的值．（2）利用同角三角函数的基本关系、及三角函数在各个象限中的符号，求得cosα的值，再利用二倍角公式、两角差的正弦公式求得要求式子的值．
【考点精析】根据题目的已知条件，利用同角三角函数基本关系的运用的相关知识可以得到问题的答案，需要掌握同角三角函数的基本关系：；;（3）倒数关系：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设函数f（x）=|x﹣a|+|x﹣5|．
（1）当a=1时，求f（x）的最小值；
（2）如果对任意的实数x，都有f（x）≥1成立，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax﹣ （a，b∈N*），f（1）= 且f（2）＜2．
（Ⅰ）求a，b的值；
（Ⅱ）判断并证明函数y=f（x）在区间（﹣1，+∞）上的单调性．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一个口袋中装有个红球且和个白球，一次摸奖从中摸两个球，两个球颜色不同则为中奖.

(1)用表示一次摸奖中奖的概率；

(2)若，设三次摸奖（每次摸奖后球放回）恰好有次中奖,求的数学期望；

(3)设三次摸奖（每次摸奖后球放回）恰好有一次中奖的概率,当取何值时，最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了得到函数y=sin（2x﹣ ）的图象，只需把正弦曲线y=sinx上所有点（）
A.向右平移个单位长度，再将所得图象上的点横坐标缩短为原来的倍，纵坐标不变
B.向左平移个单位长度，再将所得图象上的点横坐标缩短为原来的倍，纵坐标不变
C.向右平移个单位长度，再将所得图象上的点横坐标伸长为原来的2倍，纵坐标不变
D.向左平移个单位长度，再将所得图象上的点横坐标缩短为原来的2倍，纵坐标不变

查看答案和解析>>

科目：高中数学 来源： 题型：

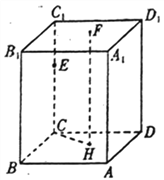
【题目】如图所示，直平行六面体中，为棱上任意一点，为底面（除外）上一点，已知在底面上的射影为，若再增加一个条件，就能得到，现给出以下条件：

①；②在上；③平面；④直线和在平面的射影为同一条直线．其中一定能成为增加条件的是__________．（把你认为正确的都填上）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为得到函数y=cos（2x+ ）的图象，只需将函数y=cos2x的图象（）
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位
D.向右平移个长度单位

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下面有命题： ①y=|sinx﹣ |的周期是π；
②y=sinx+sin|x|的值域是[0，2]；
③方程cosx=lgx有三解；
④ω为正实数，y=2sinωx在上递增，那么ω的取值范围是；
⑤在y=3sin（2x+ ）中，若f（x1）=f（x2）=0，则x1﹣x2必为π的整数倍；
⑥若A、B是锐角△ABC的两个内角，则点P（cosB﹣sinA，sinB﹣cosA在第二象限；
⑦在△ABC中，若，则△ABC钝角三角形．其中真命题个数为（）
A.2
B.3
C.4
D.5