练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有一段推理是：“直线平行于平面，则平行于平面内的所有直线；已知直线平面，直线平面，直线平面，则直线平面.”其结论显然是错误的，这是因为 （ ）

    A.使用了“三段论”，但大前提是错误的B.使用了“三段论”，但小前提是错误的

    C.使用了归纳推理D.使用了类比推理

    【答案】A

    【解析】

    本题考查的知识点是演绎推理的基本方法及空间中线面关系，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是逻辑错误，我们“直线平行于平面，则平行于平面内所有直线；已知直线平面，直线平面，直线平面，则直线直线”的推理过程，不难得到结论．

    解：直线平行于平面，则直线可与平面内的直线平行、异面、异面垂直．

    故大前提错误．

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明，得到如下列联表：

    男

    女

    总计

    读营养说明

    16

    28

    44

    不读营养说明

    20

    8

    28

    总计

    36

    36

    72

    (1)根据以上列联表判断，能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢？

    (2)从被询问的28名不读营养说明的大学生中，随机抽取2名学生，求抽到女生人数

    的分布列及数学期望.

    附：

    0.010

    0.005

    0.001

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人群中各种血型的人所占的比例见下表：

    血腥

    A

    B

    AB

    O

    该血型的人所占的比例/%

    28

    29

    8

    35

    已知同种血型的人可以互相输血，O型血可以给任一种血型的人输血，任何人的血都可以输给AB型血的人，其他不同血型的人不能互相输血.该人群中的小明是B型血，若他因病需要输血，问：

    （1）任找一个人，其血可以输给小明的概率是多少？

    （2）任找一个人，其血不能输给小明的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司在过去几年内使用某种型号的灯管1 000根，该公司对这些灯管的使用寿命（单位：h）进行了统计，统计结果如表所示：

    分组

    频数

    48

    121

    208

    223

    频率

    分组

    频数

    193

    165

    42

    频率

    （1）将各组的频率填入表中；

    （2）根据上述统计结果，估计该种型号灯管的使用寿命不足1500 h的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列对应是从集合A到集合B的映射的是（ ）

    A.集合是圆是三角形，对应关系f：每一个圆都对应它的内接三角形

    B.集合对应关系

    C.集合，对应关系f：求绝对值

    D.集合，对应关系f：开平方

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了了解学生使用手机的情况，分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图，将使用手机时间不低于80分钟的学生称为“手机迷”.

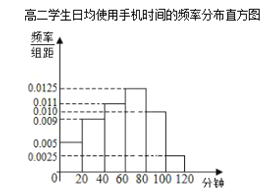
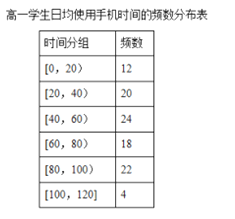
    （I）将频率视为概率，估计哪个年级的学生是“手机迷”的概率大？请说明理由.

    （II）在高二的抽查中，已知随机抽到的女生共有55名，其中10名为“手机迷”.根据已知条件完成下面的2×2列联表，并据此资料你有多大的把握认为“手机迷”与性别有关？

    非手机迷

    手机迷

    合计

    男

    女

    合计

    附：随机变量（其中为样本总量）.

    参考数据

    0.15

    0.10

    0.05

    0.025

    span>2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R．

    (1)求A∪B，(CUA)∩B；

    (2)若A∩C≠，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题共13分）

    如图，正方形ABCD和四边形ACEF所在的平面互相垂直。

    EF//AC，AB=,CE=EF=1

    （Ⅰ）求证：AF//平面BDE；

    （Ⅱ）求证：CF⊥平面BDF;

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解地区足球特色学校的发展状况，某调查机构得到如下统计数据：

    年份

    2014

    2015

    2016

    2017

    2018

    足球特色学校（百个）

    0.30

    0.60

    1.00

    1.40

    1.70

    （1）根据上表数据，计算与的相关系数，并说明与的线性相关性强弱（已知：，则认为与线性相关性很强；，则认为与线性相关性一般；，则认为与线性相关性较弱）；

    （2）求关于的线性回归方程，并预测地区2019年足球特色学校的个数（精确到个）.

    本题参考公式和数据：，，，，，.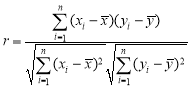

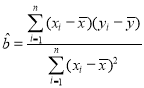    查看答案和解析>>

    同步练习册答案