
【题目】函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 在
在![]() 上单调递增时,证明:对任意
上单调递增时,证明:对任意![]() 且
且![]() .
.
【答案】(1)详见解析(2)详见解析
【解析】试题分析:(1)先求函数导数,确定导函数零点,根据两个零点大小关系分类讨论导函数符号变化规律,进而确定函数单调区间,(2)利用导数证明不等式,关键是构造恰当的目标函数,因此先利用分析法探求目标函数:第一步,根据(1)得![]() ,第二步,同除以
,第二步,同除以![]() ,将二元问题转化为一元(关于
,将二元问题转化为一元(关于![]() ),第三步,利用导数研究函数
),第三步,利用导数研究函数![]() 单调性(单调递增),第四步,根据单调性,得不等关系
单调性(单调递增),第四步,根据单调性,得不等关系![]() ,根据等价性得原不等式成立.
,根据等价性得原不等式成立.
试题分析:解:(1)![]() ,
,
![]() ,
,
令![]() 得
得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
同理,可得![]() 在
在![]() 上单调递增.
上单调递增.
当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
同理,可得![]() 在
在![]() 上单调递增.
上单调递增.
综上可知,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知,当![]() 在
在![]() 上单调递增时,
上单调递增时,![]() ,故
,故![]() .
.
不妨设![]() ,则要证
,则要证![]() ,
,
只需证![]() ,
,
即证![]() ,
,
只需证![]() ,
,
令![]() ,
,
则![]() ,不等式
,不等式![]() 可化为
可化为![]() .
.
下面证明:对任意![]() ,
,
令![]() ,即
,即![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以当
,所以当![]() 时,
时,![]() 即
即![]() ,
,
故![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
所以当![]() 时,
时,![]() ,
,
故对任意![]() ,
,![]() ,
,
所以对任意![]() 且
且![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】截止到1999年底,我国人口约为13亿,若今后能将人口平均增长率控制在1%,经过x年后,我国人口为y(单位:亿).
(1)求y与x的函数关系式y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数,并指出函数增减的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,E,F是AD上互异的两点,G,H是BC上互异的两点,由图可知,①AB与CD互为异面直线;②FH分别与DC,DB互为异面直线;③EG与FH互为异面直线;④EG与AB互为异面直线.其中叙述正确的是 ( )
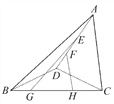
A. ①③ B. ②④ C. ①④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=
90°,BC![]()
![]() AD,BE
AD,BE![]()
![]() FA,G,H分别为FA,FD的中点.
FA,G,H分别为FA,FD的中点.
(1)证明:四边形BCHG是平行四边形.
(2)C,D,F,E四点是否共面?为什么?
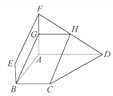
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为x;小李后掷一枚骰子,向上的点数记为y,
(1)在直角坐标系xOy中,以(x,y)为坐标的点共有几个?试求点(x,y)落在直线x+y=7上的概率;
(2)规定:若x+y≥10,则小王赢;若x+y≤4,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①线性回归方程![]() 必过点
必过点![]() ;
;
②在回归方程![]() 中,当变量
中,当变量![]() 增加一个单位时,
增加一个单位时, ![]() 平均增加5个单位;
平均增加5个单位;
③在回归分析中,相关指数![]() 为0.80的模型比相关指数
为0.80的模型比相关指数![]() 为0.98的模型拟合的效果要好;
为0.98的模型拟合的效果要好;
④在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是-7.
的值一定是-7.
其中假命题的个数是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com