
【题目】如图,在四棱锥O﹣ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离.
【答案】解:(1)由OA⊥底面ABCD,OA⊥BD.
∵底面ABCD是边长为1的正方形
∴BD⊥AC,又AC∩OA=A,∴BD⊥平面OAC
(2)设AC与BD交于点E,连结EM,则∠DME是直线MD与平面OAC所成的角,
∵MD=![]() ,DE=
,DE=![]()
∴直线MD与平面OAC所成的角为30°
(3)作AH⊥OE于点H.
∵BD⊥平面OAC
∴BO⊥AH
线段AH的长就是点A到平面OBD的距离.
∴AH=![]()
∴点A到平面OBD的距离为![]()
【解析】(1)直接证明直线BD垂直平面内的两条相交直线即可利用判定定理证明结果.
(2)设AC与BD交于点E,连结EM,则∠DME是直线MD与平面OAC所成的角,通过解三角形求解即可.
(3)作AH⊥OE于点H.说明线段AH的长就是点A到平面OBD的距离,利用三角形相似求解即可.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则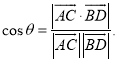 才能正确解答此题.
才能正确解答此题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组: ![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)求续驶里程在![]() 的车辆数;
的车辆数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与抛物线
与抛物线![]() 相交于不同两点
相交于不同两点![]() 、
、![]() ,与圆
,与圆![]() 相切于点
相切于点![]() ,且
,且![]() 为线段
为线段![]() 中点.
中点.
(1) 若![]() 是正三角形(
是正三角形(![]() 是坐标原点),求此三角形的边长;
是坐标原点),求此三角形的边长;
(2) 若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3) 试对![]() 进行讨论,请你写出符合条件的直线
进行讨论,请你写出符合条件的直线![]() 的条数(直接写出结论).
的条数(直接写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
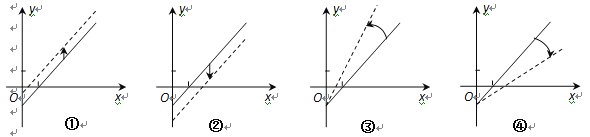
A. ①反映了建议(Ⅱ),③反映了建议(Ⅰ)
B. ①反映了建议(Ⅰ),③反映了建议(Ⅱ)
C. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
D. ④反映了建议(Ⅰ),②反映了建议(Ⅱ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
(1)求x和y的值;
(2)计算甲组7位学生成绩的方差S2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ),f(x)=
),f(x)= ![]()
![]() .
.
(1)求函数f(x)的解析式及其单调递增区间;
(2)将f(x)的图象向右平移 ![]() 个单位长度得到g(x)的图象,若g(x)﹣k≤0在区间[0,
个单位长度得到g(x)的图象,若g(x)﹣k≤0在区间[0, ![]() ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com