
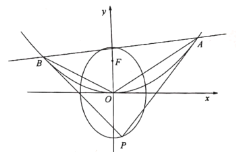
【题目】如图,已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,并以抛物线
,并以抛物线![]() :
:![]() 的焦点
的焦点![]() 为上焦点.直线
为上焦点.直线![]() :
:![]() (
(![]() )交抛物线
)交抛物线![]() 于
于![]() ,
,![]() 两点,分别以
两点,分别以![]() ,
,![]() 为切点作抛物线
为切点作抛物线![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() ,又点
,又点![]() 恰好在椭圆
恰好在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最大值;
的最大值;
(3)求证:点![]() 恒在
恒在![]() 的外接圆内.
的外接圆内.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由条件有![]() ,即
,即![]() ,由离心率可得
,由离心率可得![]() ,然后可求出
,然后可求出![]() ,得到椭圆方程.
,得到椭圆方程.
(2) 设![]() ,
,![]() ,将直线方程与抛物线方程联立,写出韦达定理,
,将直线方程与抛物线方程联立,写出韦达定理,![]() :求出直线
:求出直线![]() 的方程
的方程![]() ,同理可得
,同理可得![]() :
:![]() ,可得到
,可得到![]() ,根据点
,根据点![]() 在椭圆,得到
在椭圆,得到![]() ,利用均值不等式可到答案.
,利用均值不等式可到答案.
(3) 因为过原点![]() ,所以可设
,所以可设![]() 的外接圆方程为
的外接圆方程为![]() ,将
,将![]() ,
,![]() 坐标代入圆的方程,求出
坐标代入圆的方程,求出![]() ,将点
,将点![]() 代入外接圆方程可得
代入外接圆方程可得![]() ,从而可证.
,从而可证.
(1)解:由已知得![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,由直线
,由直线![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 方程联立可得
方程联立可得![]() ,
,
所以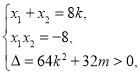
因为![]() ,所以
,所以![]() :
:![]() ,即
,即![]() :
:![]() ,
,
同理可得![]() :
:![]() ,
,
由直线![]() 的方程与直线
的方程与直线![]() 的方程联立有
的方程联立有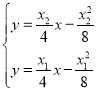 ,可得
,可得![]()
将![]() 代入直线
代入直线![]() 可得
可得![]()
所以![]() ,即
,即![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
即![]() .
.
因为![]() ,
,
所以当![]() ,
,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(3)证法:因为过原点![]() ,所以可设
,所以可设![]() 的外接圆方程为
的外接圆方程为![]() ,
,
由已知可得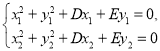
故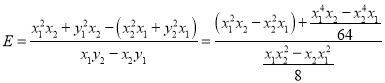
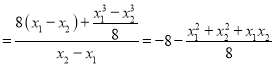 ,
,
所以![]() ,
,
将点![]() 代入外接圆方程可得
代入外接圆方程可得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以点![]() 恒在
恒在![]() 的外接圆内.
的外接圆内.
证法二:设![]() 的外心为
的外心为![]() ,
,
由已知可得![]() 的中垂线为
的中垂线为![]() ,即
,即![]() ,
,
同理![]() 的中垂线为
的中垂线为![]() ,
,
联立可得![]()
所以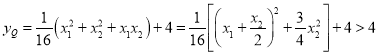 ,
,
又因为![]() ,
,![]() ,
,
所以![]() ,
,
所以点![]() 恒在
恒在![]() 的外接圆内.
的外接圆内.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在![]() 的客户称为“熟客”,并把他们去年采购的数量制成下表:
的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x |
|
|
|
|
|
客户数 | 10 | 10 | 5 | 20 | 5 |
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的![]() ,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元(![]() )销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
)销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() ,以坐标原点O为极点,
,以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足|
于点M,点N为射线OM上的点,满足| ![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(1)①设动点![]() ,记
,记![]() 是直线
是直线![]() 的向上方向的单位方向向量,且
的向上方向的单位方向向量,且![]() ,以t为参数求直线
,以t为参数求直线![]() 的参数方程
的参数方程
②求曲线C的极坐标方程并化为直角坐标方程;
(2)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意连续三项
对任意连续三项![]() ,均有
,均有![]() ,则称该数列为“跳跃数列”.
,则称该数列为“跳跃数列”.
(1)判断下列两个数列是否是跳跃数列:
①等差数列:![]() ;
;
②等比数列:![]() ;
;
(2)若数列![]() 满足对任何正整数
满足对任何正整数![]() ,均有
,均有![]()
![]() .证明:数列
.证明:数列![]() 是跳跃数列的充分必要条件是
是跳跃数列的充分必要条件是![]() .
.
(3)跳跃数列![]() 满足对任意正整数
满足对任意正整数![]() 均有
均有![]() ,求首项
,求首项![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
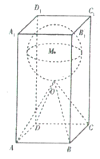
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
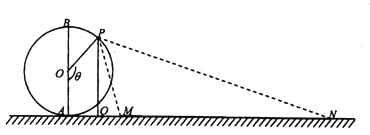
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com