Question

【题目】已知函数（，）的一系列对应值如表：

（1）根据表格提供的数据求函数的一个解析式；

（2）根据（1）的结果：

①当时，方程恰有两个不同的解，求实数的取值范围；

②若，是锐角三角形的两个内角，试比较与的大小．

Answer 1

【答案】（1）；（2）①；②.

【解析】

试题分析：（1）由表格知函数的周期是，所以，根据最大值和最小值，求得，代入求得，因此，；（2）①，画出的图象，根据图象求得的取值范围；②由于，即，在上单调递增，所以.

试题解析：

（1）设的最小正周期为，则由表格可得，

再根据，解得，故，

又当时，，，

即

（），即（），

取，得，

因此，；……………（4分）

（2）①由已知，

，，

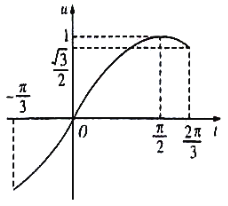
由图知，若在上有两个不同的解，则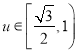

方程在时恰好有两个不同的解，则，即实数的取值范围是．………………………（8分）

②、是锐角三角形的两个内角，，即，

又在上单调递增，

，即且，，

再由得，

在上单调递增，故在上单调递增．

因此．…………………………………（12分）