
����Ŀ��(��С������![]() ��)��֪Բ
��)��֪Բ![]() ���������ʣ�
���������ʣ�
����Բ![]() ��һ��
��һ��![]() ��Բ�����߷�����
��Բ�����߷�����![]() .
.
����![]() ΪԲ
ΪԲ![]() ��һ�㣬��
��һ�㣬��![]() ��Բ
��Բ![]() ���������ߣ��е�ֱ�Ϊ
���������ߣ��е�ֱ�Ϊ![]() ����ֱ��
����ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
���������������ϵĵ�![]() ΪԲ
ΪԲ![]() ��һ�㣬��
��һ�㣬��![]() ��Բ
��Բ![]() ���������ߣ��е�ֱ�Ϊ
���������ߣ��е�ֱ�Ϊ![]() ����
����![]() ��ֱ
��ֱ![]() ����
����![]() ����
����![]() ƽ���߶�
ƽ���߶�![]() .
.
(1)��������йؽ��ۣ��������Բ![]() ��һ��
��һ��![]() �����߷���(��Ҫ��֤��)��
�����߷���(��Ҫ��֤��)��
(2)����Բ![]() ��һ��
��һ��![]() ����ֱ�ߣ�����Բ������
����ֱ�ߣ�����Բ������![]() ���㣬���
���㣬���![]() �����ֱ�߷��̣�
�����ֱ�߷��̣�
(3)������Բ![]() ��һ��
��һ��![]() ��
��![]() �����������ϣ�����ֱ�ߣ�����Բ������
�����������ϣ�����ֱ�ߣ�����Բ������![]() ���㣬��֤��
���㣬��֤��![]() Ϊ��ֵ����
Ϊ��ֵ����![]() ƽ���߶�
ƽ���߶�![]() .
.
���𰸡���1��![]()
��2��![]()
(3)������.
����������������1��������������ɵý��ۣ���2����![]() ����ϣ�1���ɵù���
����ϣ�1���ɵù���![]() �����߷��̣����������߶�����
�����߷��̣����������߶�����![]() �ɵ�
�ɵ�![]() ��
��![]() ���ٽ�Ϲ������ֱ��Ψһ���ص�ɵ�ֱ��
���ٽ�Ϲ������ֱ��Ψһ���ص�ɵ�ֱ��![]() �ķ�����
�ķ�����![]() ����3������ֱ��
����3������ֱ��![]() �ķ��̿ɵ�
�ķ��̿ɵ�![]() ����
����![]() ������
������![]() �����߶�
�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ���ɵ���
���ɵ���![]() ������
������![]() ����
����![]() ������
������![]() ���㹲�ߣ��Ӷ��õ�
���㹲�ߣ��Ӷ��õ�![]() ƽ���߶�
ƽ���߶�![]() ��
��
��⣺��1������Բ![]() ��һ��
��һ��![]() �����߷�����
�����߷�����![]() ��
��
��2����![]() ��
��
�ɣ�1���ù���Բ�ϵ�![]() ������
������![]() �ķ�����
�ķ�����![]() ��
��
��ֱ��![]() ����
����![]() ��
��
��![]() ��
��
ͬ��![]() ��
��
�ֹ�����A,B��ֱ����Ψһ�ģ�
��ֱ��![]() �ķ�����
�ķ�����![]() ��
��
��3���ɣ�2��֪��![]() �����ֱ�߷�����
�����ֱ�߷�����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() Ϊ��ֵ��
Ϊ��ֵ��
��![]() �߶�
�߶�![]() ���е�Ϊ
���е�Ϊ![]() ����
����![]() ��
��
�ߵ�![]() ������Բ�ϣ�
������Բ�ϣ�
��![]() ����
����![]() ��
��
�����ٵ�![]() ��
��
��![]() ��
��
��![]() ��
��
��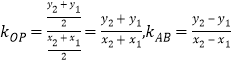
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ���㹲����
���㹲����
��![]() ƽ���߶�
ƽ���߶�![]() ��
��


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������������У�ƽ��
Ϊ������������У�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ���ı���
���ı���![]() Ϊƽ���ı��Σ���
Ϊƽ���ı��Σ���![]() .
.
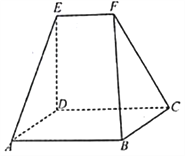
��1����֤��![]() ��
��
��2����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽ�Ϊ
���ɽ�Ϊ![]() ����ƽ��
����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ.
���������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ���ϵ�![]() ����������
����������![]() ��
�� ![]() �ľ���֮�ȵ���5.
�ľ���֮�ȵ���5.
��1�����![]() �Ĺ켣���̣���˵���켣��ʲôͼ�Σ�
�Ĺ켣���̣���˵���켣��ʲôͼ�Σ�
��2���ǣ�1���еĹ켣Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
��![]() ���صõ��߶εij�Ϊ 8����ֱ��
���صõ��߶εij�Ϊ 8����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() Ϊ��Ȼ�����ĵ�������������
Ϊ��Ȼ�����ĵ�������������![]() �ڵ�
�ڵ�![]() ��������ƽ����
��������ƽ����![]() ��.
��.
��1����![]() ��ֵ��
��ֵ��
��2������![]() �ļ�ֵ.
�ļ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��a��0��a��1�����溯����
��a��0��a��1�����溯����
��1����ʵ��m��ֵ��
��2���жϺ���f��x���ڣ�1��+�ޣ��ϵĵ����ԣ�������֤����
��3����x�ʣ�n��a��2��ʱ������f��x����ֵ���ǣ�1��+�ޣ�����ʵ��a��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|x2��2x��3��0��x��R}��B={x|m��1��x��m+1��x��R��m��R}
��1����A��B=[1��3]����ʵ��m��ֵ��
��2����ARB����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��![]() Ϊ��������������ԭ��Ϊ���㣬
Ϊ��������������ԭ��Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��
���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]()
��1����![]() ʱ���ж�ֱ��
ʱ���ж�ֱ��![]() ��Բ
��Բ![]() �Ĺ�ϵ��
�Ĺ�ϵ��
��2����![]() ������ֻ��һ�㵽ֱ��
������ֻ��һ�㵽ֱ��![]() �ľ������
�ľ������![]() ʱ����
ʱ����![]() �ϵ�ֱ��
�ϵ�ֱ��![]() ����Ϊ
����Ϊ![]() �ĵ�����꣮
�ĵ�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ����f��x��=mn�� ��I����f��x���ĵ����������䣻
����f��x��=mn�� ��I����f��x���ĵ����������䣻
��II����֪��ABC�����ڽ�A��B��C�Ա߷ֱ�Ϊa��b��c����a=3��f ![]() ��sinC=2sinB����A��c��b��ֵ��
��sinC=2sinB����A��c��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������ij���Ϊ������ɫ���С��ṩ�˼���ķ��㣬ij����������˾��Mobike���ƻ��ڼס����������й�Ͷ��120��Ԫ��������ҵ�涨��ÿ����������ҪͶ��40��Ԫ����ǰ���г����п�֪���׳�������P��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ���ҳ�������Q��Ͷ��
���ҳ�������Q��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ����׳��е�Ͷ��Ϊ
����׳��е�Ͷ��Ϊ![]() ����λ����Ԫ�����������е�������Ϊ
����λ����Ԫ�����������е�������Ϊ![]() ����λ����Ԫ����
����λ����Ԫ����
��1�����׳���Ͷ��50��Ԫʱ�����ʱ��˾�����棻
��2��������ΰ��żס����������е�Ͷ�ʣ�����ʹ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com