
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
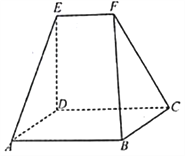
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,则
,则![]() .则
.则![]() ,
,![]() ,
,![]() 为等腰直角三角形,据此可得
为等腰直角三角形,据此可得![]() 平面
平面![]() ,
,![]() .
.
(2)以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,由题设可得平面
,由题设可得平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则锐二面角的余弦值为
,则锐二面角的余弦值为
![]() .
.
试题解析:
(1)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由平面
,由平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,因此
,因此![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由已知![]() 得
得![]() 为等腰直角三角形,因此
为等腰直角三角形,因此![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
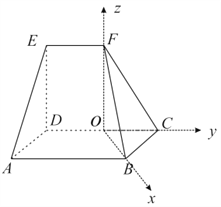
(2)∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵平面![]() 平面
平面![]() ,∴
,∴![]() ,
,
由(1)可得![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,由题设可得
,由题设可得![]() ,进而可得
,进而可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() ,
,
可取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() ,
,
可取![]() ,
,
则
![]() ,
,
∴二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
![]() 恰好有3个零点, 等价于
恰好有3个零点, 等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,根据数形结合可得结果.
的图象,根据数形结合可得结果.

![]() 恰好有3个零点,
恰好有3个零点,
等价于![]() 有三个根,
有三个根,
等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,如图,
的图象,如图,
由图可知,
当![]() 时,
时,![]() 的图象有三个交点,
的图象有三个交点,
即当![]() 时,
时,![]() 恰好有3个零点,
恰好有3个零点,
所以,![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.
【点睛】
本题主要考查函数的零点与分段函数的性质,属于难题. 函数的性质问题以及函数零点问题是高考的高频考点,考生需要对初高中阶段学习的十几种初等函数的单调性、奇偶性、周期性以及对称性非常熟悉;另外,函数零点的几种等价形式:函数![]() 的零点
的零点![]() 函数
函数![]() 在
在![]() 轴的交点
轴的交点![]() 方程
方程![]() 的根
的根![]() 函数
函数![]() 与
与![]() 的交点.
的交点.
【题型】单选题
【结束】
13
【题目】设集合A={0,log3(a+1)},B={a,a+b}若A∩B={1},则b=______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=k(x﹣m)与抛物线y2=2px(p>0)交于A、B两点,O为坐标原点,OA⊥OB,OD⊥AB于D,点D在曲线x2+y2﹣4x=0上,则p= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)满足:对y=f(x)图象上任意点P(x1 , f(x1)),总存在点P′(x2 , f(x2))也在y=f(x)图象上,使得x1x2+f(x1)f(x2)=0成立,称函数y=f(x)是“特殊对点函数”,给出下列五个函数:
①y=x﹣1;
②y=log2x;
③y=sinx+1;
④y=ex﹣2;
⑤y= ![]() .
.
其中是“特殊对点函数”的序号是(写出所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ).
).
(1)利用“五点法”,完成以下表格,并画出函数f(x)在一个周期上的图象;
(2)求函数f(x)的单调递减区间和对称中心的坐标;
(3)如何由y=cosx的图象变换得到f(x)的图象.
2x- | 0 |
| π |
| 2π |
x | |||||
f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,
DC, ![]() .
.
(1)求证:AE∥平面PBC;
(2)求证:AE⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P 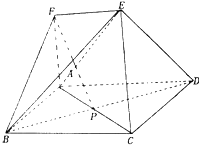
(1)证明:PF∥面ECD;
(2)求二面角B﹣EC﹣A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)已知圆
分)已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
③若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() ,且
,且![]() 平分线段
平分线段![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程(不要求证明);
的切线方程(不要求证明);
(2)过椭圆![]() 外一点
外一点![]() 作两直线,与椭圆相切于
作两直线,与椭圆相切于![]() 两点,求过
两点,求过![]() 两点的直线方程;
两点的直线方程;
(3)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值,且
为定值,且![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com