
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【答案】
(1)解:∵f(x)=sin2xcos ![]() +cos2xsin
+cos2xsin ![]() +sin2xcos
+sin2xcos ![]() ﹣cos2xsin
﹣cos2xsin ![]() +cos2x
+cos2x
=sin2x+cos2x
= ![]() sin(2x+
sin(2x+ ![]() ),
),
∴函数f(x)的最小正周期T= ![]() =π
=π
(2)解:∵函数f(x)在区间[ ![]() ]上是增函数,在区间[
]上是增函数,在区间[ ![]() ,
, ![]() ]上是减函数,
]上是减函数,
又f(﹣ ![]() )=﹣1,f(
)=﹣1,f( ![]() )=
)= ![]() ,f(
,f( ![]() )=1,
)=1,
∴函数f(x)在区间[ ![]() ]上的最大值为
]上的最大值为 ![]() ,最小值为﹣1
,最小值为﹣1
【解析】(1)利用正弦函数的两角和与差的公式与辅助角公式将f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1化为f(x)=
)+2cos2x﹣1化为f(x)= ![]() sin(2x+
sin(2x+ ![]() ),即可求得函数f(x)的最小正周期;(2)可分析得到函数f(x)在区间[
),即可求得函数f(x)的最小正周期;(2)可分析得到函数f(x)在区间[ ![]() ]上是增函数,在区间[
]上是增函数,在区间[ ![]() ,
, ![]() ]上是减函数,从而可求得f(x)在区间[
]上是减函数,从而可求得f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.


科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点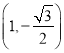 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2-e2x.
(1)若曲线y=f(x)在点(2,f(2))处的切线平行于x轴,求函数f(x)的单调区间;
(2)若x>0时,总有f(x)>-e2x,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条不重合的直线![]() 和两个不重合的平面
和两个不重合的平面![]() ,若
,若![]() ,则下列四个命题:①若
,则下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ; ③若
; ③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() ,其中正确命题的个数是( )
,其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)满足:对任意x∈R,都有f(x+1)+f(x)=2x2﹣2x﹣3
(1)求f(x)的解析式;
(2)若关于x的方程f(x)=a有两个实数根x1 , x2 , 且满足:﹣1<x1<2<x2 , 求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,又数列{ ![]() }(n∈N*)是公差为1的等差数列.
}(n∈N*)是公差为1的等差数列.
(1)求数列{an}的通项公式an;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com