
【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
(1)如图1,作![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() .
.
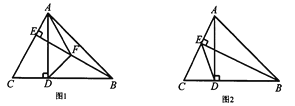
①依据题意补全图形;
②用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
【答案】(1)证明见解析;(2)①图形见解析;②![]() ,证明见解析.
,证明见解析.
【解析】
试题分析:(1)要证![]() 由
由![]() 推出
推出![]() 即可解决问题;(2)①根据条件画出图形即可;②数列关系是
即可解决问题;(2)①根据条件画出图形即可;②数列关系是![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,先证明
,先证明![]() ,在证明四边形
,在证明四边形![]() 是平行四边形,即可解决问题.
是平行四边形,即可解决问题.
试题解析:(1)∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,………………………………1分;
,………………………………1分;
∵![]() 平分
平分![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,∵
中,∵ ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() ……………………3分;或用“三线合一”
……………………3分;或用“三线合一”
(2)补全图形………………4分;数量关系是:![]() .………………4分
.………………4分

过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,∵
中,∵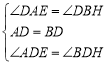 ,∴
,∴![]() ,
,
∴![]() ,
,![]() .…………………………8分
.…………………………8分
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,∴
对称,∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
∴![]() .…………………………12分
.…………………………12分
或过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
①函数关系是一种确定性关系;
②相关关系是一种非确定性关系;
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;
④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过原点
为圆心的圆过原点![]() .
.
(1)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)在(1)的条件下,设![]() ,且
,且![]() 分别是直线
分别是直线![]() 和圆
和圆![]() 上的动点,求
上的动点,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来确定推断“X与Y有关系”的可信度,如果k>5.024,那么就推断“X和Y有关系”,这种推断犯错误的概率不超过( )
A. 0.25 B. 0.75
C. 0.025 D. 0.975
查看答案和解析>>
科目:高中数学 来源: 题型:
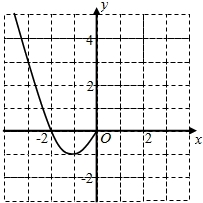
【题目】已知函数是定义在上的偶函数,且当时,.
(1)现已画出函数在轴左侧的图象,如图所示,请补出完整函数的图象,并根据图象写出函数的增区间;
(2)写出函数的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于“斜二测”直观图的画法,下列说法中正确的是( )
A. 等腰三角形的直观图仍为等腰三角形; B. 圆的直观图仍为圆;
C. 正方形的直观图为平行四边形; D. 梯形的直观图不是梯形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com