
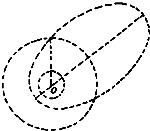
 宇宙飞船在距火星表面H高度处作匀速圆周运动,火星半径为R,今设飞船在极短时间内向外侧点喷气,使飞船获得一径向速度,其大小为原速度的α倍,因α量很小,所以飞船新轨道不会与火星表面交会,如图所示,飞船喷气质量可忽略不计.
宇宙飞船在距火星表面H高度处作匀速圆周运动,火星半径为R,今设飞船在极短时间内向外侧点喷气,使飞船获得一径向速度,其大小为原速度的α倍,因α量很小,所以飞船新轨道不会与火星表面交会,如图所示,飞船喷气质量可忽略不计.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| Mm |
| r |
| 1 |
| 2 |
| v | 2 0 |
| v | 2 0 |
| Mm |
| r0 |
| Mm | ||
|
| ||
| r0 |
| r | 2 0 |
|
| H-αR |
| 1+α |
| H+αR |
| 1-α |
| r0 |
| 1-α2 |
| 2πr0 |
| v0 |
| T |
| T0 |
| a |
| r0 |
| a |
| r0 |
| 2πr0 |
| v0 |
| 1 |
| 1-α2 |
| 2π(R+H) |
| v0 |
| 1 |
| 1-α2 |
| H-αR |
| 1+α |
| H+αR |
| 1-α |
| 2π(R+H) |
| v0 |
| 1 |
| 1-α2 |


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中物理 来源:2007年江苏省高考物理预测试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com