
1.设某等差数列的首项为a(a≠0),第二项为b.则这个数列中有一项为0的充要条件是
A.a-b是正整数 B.a+b是正整数
C. D.
D.  是正整数
是正整数
2.已知b≠0,则b= 是a、b、c成等比数列的
是a、b、c成等比数列的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,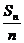 ),Q(n+2,
),Q(n+2, )(n∈N*)的一次函数解析式是
)(n∈N*)的一次函数解析式是
A.y=2x+1
B.y=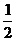 C.y=
C.y=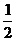 x-1 D.y=2x-1
x-1 D.y=2x-1
4.若数列{an}的通项公式为an=5( )2n-2 -4(
)2n-2 -4( )n-1(n∈N*),{an}的最大项为第x项,最小项为第y项,则x+y等于
)n-1(n∈N*),{an}的最大项为第x项,最小项为第y项,则x+y等于
A.3 B.4 C.5 D.6
5. 已知an= (n∈N*),则数列{an}的最大项为
(n∈N*),则数列{an}的最大项为
A.a12 B.a13 C.a12或a13 D.不存在
6.等比数列{an}中,a1=512,公比q=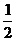 ,用Πn表示它的前n项之积:Πn=a1.a2.….an,则Π1,Π2…中最大的是
,用Πn表示它的前n项之积:Πn=a1.a2.….an,则Π1,Π2…中最大的是
A.Π12 B.Π11 C.Π9 D.Π8
7.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为

A. an=3n-1 B.an=3n C.an=3n -2n D.an=3n-1+2n-3
8.某人从2002年1月1日起,且以后每年1月1日到银行存入a元(一年定期),若年利
率r保持不变,且每年到期后存款均自动转为新一年定期,到2008年1月1日将所有存款及利息全部取回,他可取回的钱数(单位为元)为
A.a(1+r)7
B.  [(1+r)7-(1+r)]
[(1+r)7-(1+r)]
C.a(1+r)8
D.  [(1+r)8-(1+r)]
[(1+r)8-(1+r)]
第Ⅱ卷(非选择题,共60分)
9.在等比数列{an}中,a1+a2+a3= -3,a1.a2.a3=8,且a1>a3,则an= .
10.已知数列{an}的前n项和Sn= ,则数列{
,则数列{ }的前n项和Tn=
.
}的前n项和Tn=
.
11.在n行m列的方格表中每个方格上都填上一个数,使得第n行的m个数与每列的n个数分别都成等差数列,如果表的角上的四个数的和等于s,则这个表中所有数的和等于 .
12.某些植物发芽具有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽,如下表(设第一年前的新芽数为a):
|
第x年 |
1 |
2 |
3 |
4 |
5 |
… |
|
老芽数 |
a |
A |
2a |
3a |
5a |
… |
|
新芽数 |
0 |
A |
A |
2a |
3a |
… |
|
总芽数 |
a |
2a |
3a |
5a |
8a |
… |
照这样下去,第8年老芽数与总芽数的比值为 (精确到0.001).
13. (本小题满分12分)
已知等差数列{an}中,a2=8,前10项的和S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺序排列成一个新的
数列{bn},试求新数列{bn}的前n项和An.
14. (本小题满分12分)
为了保护三峡库区的生态环境,凡是坡度在25°以上的坡荒地都要绿化造林,经初步统计,在三峡库区坡度大于25°的坡荒地面积约为2640万亩,若从2003年初开始绿化造林,第一年造林120万亩,以后每一年都比前一年多绿化60万亩.
(1)若所有应被绿化造林的坡荒地全部绿化成功,问到哪一年底可使库区的坡荒地全部绿化?
(2)若每万亩绿化造林所植树苗的木材量平均为0.1万立方米,每年树木木材量的自然增长率为20%,那么当整个库区25°以上荒地全部绿化完的哪一年底,一共有木材多少万立方米?(保留1位小数,1.29=5.16,1.28=4.30)
15. (本小题满分12分)
设等差数列{an}的首项为a(a≠0),公差为2a,前n项和为Sn.记A={(x,y)|x=n,y= ,n∈N*},B={(x,y)|(x-2)2+y2=1,x、y∈R}.
,n∈N*},B={(x,y)|(x-2)2+y2=1,x、y∈R}.
 (1)若A∩B≠ ,求a的取值集合;
(1)若A∩B≠ ,求a的取值集合;
(2)设点P∈A,点Q∈B,当a=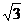 时,求|PQ|的最小值.
时,求|PQ|的最小值.
16. (本小题满分12分)
已知函数f(x)的定义域为[0,1],且同时满足:
①对任意x∈[0,1],总有f(x)≥2;②f(1)=3;③若x1≥0,x2≥0且x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-2.
(1)求f(0)的值;
(2)试求f(x)的最大值;
(3)设数列{an}的前n项和为Sn,且满足a1=1,Sn= -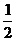 (an-3),n∈N*.
(an-3),n∈N*.
求证:f(a1)+f(a2)+…+f(an)≤ +2n-
+2n- .
.
高考数学复习数列测试题 第Ⅰ卷(选择题,共40分)参考答案
参考答案
1. D an=a+(n-1)(b-a)=0,n-1= 是正整数.故选D.
是正整数.故选D.
2. A 当b≠0时,a、b、c成等比数列 b2=ac
b2=ac b=±
b=± .
.
 3.A {
3.A {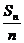 }也成等差,故一次函数过点(2,
}也成等差,故一次函数过点(2, ),(5,
),(5, ).
).
4.Aan=5( )2n – 2 -4(
)2n – 2 -4( )n –1 (n∈N*)令u=(
)n –1 (n∈N*)令u=( )n-1(n∈N*),则u=1,
)n-1(n∈N*),则u=1, ,
, ,…则an=5.u2-4u.
,…则an=5.u2-4u.
如图,当u=1时an取得最大项,即第一项:x=1.
当u= 时,an取得最小项,即第二项:y=2,则有x+y=3.故选A.
时,an取得最小项,即第二项:y=2,则有x+y=3.故选A.
5.C法Ⅰ:考察函数f(x)=x+ (x>0)知,当且仅当x=
(x>0)知,当且仅当x= 时,f(x)有最小值,且当x>
时,f(x)有最小值,且当x> 时单增,0<x<
时单增,0<x< 时单减,又12<
时单减,又12< <13,而f(12)=f(13)=25.故当n=12或13时,n+
<13,而f(12)=f(13)=25.故当n=12或13时,n+ 取最小值25,而an有最大值
取最小值25,而an有最大值 .
.
法Ⅱ:由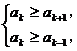 得
得 即
即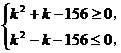
∴1-2≤k≤13,即当n=12或13时,an最大.
点评:要确定数列最大项,一种思路是判定数列的单调性(比较an与an-1大小),一种思路是借助函数的单调性及最值求法.
6.Can=210 – n ,Πn=29+8+…+(10–n)= .
.
7. A 由题意分析知:a1=1,a2=3,a3=9,a4=27,则数列{an}可以是首项为a1=1,公比q=3的等比数列,所以an=a1.qn-1=3n-1.故选A.
8.B2007年1月1日,2006年1月1日,…,2002年1月1日存入钱的本息分别为:a(1+r),a(1+r)2,…,a(1+r)6.相加即可.
9.-(-2)n-1
10. an=Sn-Sn-1=n(n+1),∴
an=Sn-Sn-1=n(n+1),∴ =
= -
- .
.
11.  设
设 是题设的数表,它的第一行的数之和是a11+a12+…+a1m=
是题设的数表,它的第一行的数之和是a11+a12+…+a1m= ;
;
第n行的数之和为an1+an2+…+anm= ;
;
各列的数的和依次为 ,
, ,…,
,…, .
.
设表中所有的数的和为Snm,则Snm= +
+  +…+
+…+ =[(a11+an1)+(a12+an2)+…+(a1m+anm)]×
=[(a11+an1)+(a12+an2)+…+(a1m+anm)]×
=[(a11+a12+a1m)+(an1+an2+…+anm)×
= +
+ ×
×
=(a11+a1m+an1+anm)× =
= .
.
点评:本题为数列与矩阵结合题,要求所有数的和,只需根据等差数列前n项和公式Sn= ,将所有数的和转化为已知条件四个角上的数的和s即可.
,将所有数的和转化为已知条件四个角上的数的和s即可.
12.0.618 从表中易推得第8年老芽数为21a,总芽数为34a.
事实上设老芽数为数列{an},则知an+1=an+an-1.
点评:本题以菲波那契“兔子数列”及黄金分割为背景设计,可让学生感知数学应用无处不在,数学美无处不在.
13.解:(1)an=3n+2
(2)bn= =3.2n+2,则An=3(2+22+…+2n)+2n=6(2n-1)+2n=6.2n+2n-6.
=3.2n+2,则An=3(2+22+…+2n)+2n=6(2n-1)+2n=6.2n+2n-6.
14.解:(1)设a1=120,d=60,第n年后可以使绿化任务完成,则有Sn=120n+ .60≥2640,解得n≥8.故到2010年底,可以使库区内25°以上的坡地全部绿化.
.60≥2640,解得n≥8.故到2010年底,可以使库区内25°以上的坡地全部绿化.
(2)到2010年造林数量为a8=120+7×60=540(万亩),
设到2010年木材总量为S,依题意有:
S=(120×1.28+180×1.27+240×1.26+…+540×1.2)×0.1
=6(2×1.28+3×1.27+…+9×1.2)
则1.2S=6(2×1.29+3×1.28+…+9×1.22)
两式相减,有:0.2S=6(2×1.29+1.28+1.27+…+1.22-9×1.2)
=6[2×1.29+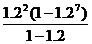 -10.8]=6(7×1.29-18)
-10.8]=6(7×1.29-18)
∴S=30(7×1.29-18)≈543.6(万立方米)
答:到2010年底共有木材543.6万立方米.
点评:本题具有浓郁的时代特色,解答的过程不仅涉及抽象建模,等差、等比数列及错位相减求和等知识方法的应用,还能从中体会到数学的科学价值和人文价值.
15.解:(1)由已知得Sn=na+ .2a=an2,
.2a=an2, 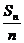 =an.
=an.
∴A={(x,y)|y=ax,x∈N*}.(a≠0)
由B={(x,y)|(x-2)2+y2=1,x,y∈R}知|x-2|≤1 ∴1≤x≤3.
 由A∩B≠ ,知集合B中x只能取1,2,3,又y≠0,∴x=2.
由A∩B≠ ,知集合B中x只能取1,2,3,又y≠0,∴x=2.
此时y=±1,由y=ax可求得a=±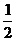 . 故a的取值集合为{
. 故a的取值集合为{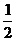 ,-
,-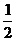 }.
}.
(2)由(1)知点P可设为(n,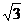 n),圆(x-2)2+y2=1的圆心M(2,0),半径r=1.先求|PM|最小值. |PM|2=(n-2)2+3n2=4n2-4n+4=4(n-
n),圆(x-2)2+y2=1的圆心M(2,0),半径r=1.先求|PM|最小值. |PM|2=(n-2)2+3n2=4n2-4n+4=4(n-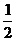 )2+3.
)2+3.
又n∈N*,∴|PM|最小值为2(n=1).
故|PQ|min=|PM|min-r=2-1=1.
点评:本题在数列、函数、直线与圆、集合等知识交汇处立意,考查学生综合分析问
题能力,关键在于深刻理解离散函数y=ax,x∈N*,连续函数y=ax,x∈R在与圆位置关系中的不同点.另外,可借助图象加以分析.
16. (1)令x1=x2=0,则f(0)≥2f(0)-2,∴f(0)≤2.又对任意x∈[0,1],总有f(x)≥2,∴f(0)=2.
(2)任取x1,x2∈[0,1]且x1<x2,则0<x2-x1≤1,∴f(x2-x1)≥2.∴f(x2)=f(x2-x1+x1)≥f(x2-x1)+f(x1)-2≥f(x1),∴f(x)的最大值为f(1)=3.
(3)∵Sn= -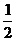 (an-3)(n∈N*),∴Sn-1= -
(an-3)(n∈N*),∴Sn-1= -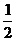 (an-1-3)(n≥2),
(an-1-3)(n≥2),
∴an=
-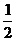 an+
an+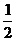 an-1(n≥2).∴an=
an-1(n≥2).∴an= an-1(n≥2),又∵a1=1≠0,∴
an-1(n≥2),又∵a1=1≠0,∴ =
= (n≥2),∴数列{an}是以1为首项,公比为
(n≥2),∴数列{an}是以1为首项,公比为 的等比数列,∴an=
的等比数列,∴an= .
.
当n=1时,f(a1)=f(1)=3= +2-
+2-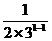 不等式成立.当n=2时,f(a2)=f(
不等式成立.当n=2时,f(a2)=f( ),
),
∵f(1)=f( +
+ +
+ )≥f(
)≥f( )+f(
)+f( +
+ )-2≥3f(
)-2≥3f( )-4.∴f(
)-4.∴f( )≤
)≤ .
.
∴f(a1)+f(a2)=f(1)+f( )≤3+
)≤3+ =
= +
+ =
= +4-
+4- 不等式成立.
不等式成立.
假设n=k时,不等式成立,即f(a1)+f(a2)+…+f(ak)≤ +2k-
+2k-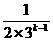 ,
,
则n=k+1时,f(ak+1)=f( )=f(
)=f( +
+ +
+ )≥3f(
)≥3f( )-4,∴f(
)-4,∴f( )≤
)≤ f(
f( )+
)+ ,f(
,f( )≤
)≤ f(
f( )+
)+ ,k=1,2,…
,k=1,2,…
∴f( )≤
)≤ f(
f(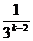 )+
)+ +
+ ≤…≤
≤…≤ f(
f( )+
)+ +
+ +…+
+…+ +
+ ≤
≤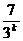 +2-
+2-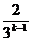 =2+
=2+ .
.
∴f(a1)+f(a2)+…+f(ak)+f(ak+1)≤ +2k-
+2k-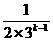 +2+
+2+ =
= +2(k+1)-
+2(k+1)-  .
.
∴n=k+1时,不等式成立.∴对n∈N*,f(a1)+f(a2)+…+f(an)≤ +2n-
+2n- .
.
另法:只要证f(an)=f( )≤
)≤ +2,然后累加即得.
+2,然后累加即得.