2009届山东省实验中学高三年级第四次综合测试
数学理科卷
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间为120分钟.
2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上.考试结束,试题
和答题卡一并收回.
3.第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)
涂黑,如需改动,必须先用橡皮擦干净,再改涂其它答案.
第Ⅰ卷 (共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
1.定义 若
若 ,
,
试题详情
 等于 ( )
等于 ( )
A.{1,2,3,4,5} B.{2,3}
C.{1,4,5} D.{6}
试题详情
2.复数 (
( 是虚数单位)在复平面上对应的点位于 ( )
是虚数单位)在复平面上对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
试题详情
3.给出如下三个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③四个实数a、b、c、d依次成等比数列的必要而不充分条件是ad=bc;
试题详情
④在△ 中,“
中,“ ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件.
其中不正确的命题的个数是 ( )
A.4 B.3 C.2 D.1
试题详情
试题详情
试题详情
5.在对两个变量x,y进行线性回归分析时,有下列步骤:
试题详情
①对所求出的回归直线方程作出解释; ②收集数据
③求线性回归方程; ④求相关系数;
⑤根据所搜集的数据绘制散点图.
如果根据可形性要求能够作出变量x,y具有线性相关结论,则在下列操作顺序中正确的
是 (
)
A.①②⑤③④ B.③②④⑤① C.②④③①⑤ D.②⑤④③①
|
试题详情
的焦点分成 的两段,则此双曲线的离心率为 ( ) 的两段,则此双曲线的离心率为 ( ) 试题详情
试题详情
试题详情
 的最大值为 ( ) 的最大值为 ( ) A.11 B.19 C.
20 D.21 试题详情
8.某服装加工厂某月生产 、 、 、 、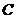 三种产品共4000件,为了保证产品质量,进行抽样检 三种产品共4000件,为了保证产品质量,进行抽样检 验,根据分层抽样的结果,企业统计员制作了如下的统计表格: 产品类别 试题详情
试题详情
试题详情
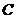
产品数量(件) 2300 样本容量(件) 230 试题详情
试题详情
本容量比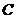 产品的样本容量多 产品的样本容量多 ,根据以上信息,可得 ,根据以上信息,可得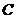 的产品数量是 ( ) 的产品数量是 ( ) A.80
B. 800 C.90 D.900 试题详情
试题详情
足 ,则实数 ,则实数 的值 ( ) 的值 ( ) 试题详情
A.2 B.-2 C. 或- 或- D.2或-2 D.2或-2 试题详情
10.某企业打算在四个候选城市投资四个不同的项目,规定在同一个城市投资的项目不超过 两个,则该外商不同的投资方案有 ( ) 试题详情
 A.24 B.96 C.240 D.384 A.24 B.96 C.240 D.384
试题详情
11.如图所示,墙上挂有边长为 的正方形木板,它的四个角的空白部 的正方形木板,它的四个角的空白部 试题详情
分都是以正方形的顶点为圆心,半径为 的圆孤,某人向此板投镖, 的圆孤,某人向此板投镖, 假设每次都能击中木板,且击中木板上每个点的可能性都一样,则 它击中阴影部分的概率是
( ) 试题详情
试题详情
试题详情
增,若 且 且 ,则 ,则 的值 ( ) 的值 ( ) A.恒大于0 B.恒小于0 C.可能等于0 D.可正可负 试题详情
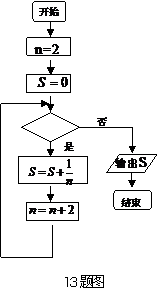
第Ⅱ卷
|
|
|
试题详情
二、填空题:本大题共4小题,每小题4分,共16分. 13.如右图所示,这是计算 的值的一 的值的一 个程序框图,其中判断框内应填入的条件是 . 试题详情
14.如果 的展开式中含有非零常数项,则正 的展开式中含有非零常数项,则正 试题详情
整数 的最小值为__________. 的最小值为__________. 试题详情
15.设不等式组 所表示的平面区域为S,若A、B为S内的两个点,则|AB|的 所表示的平面区域为S,若A、B为S内的两个点,则|AB|的 最大值为
. 试题详情
试题详情
①存在实数 ,使 ,使 ; ; 试题详情
②存在实数 ,使 ,使 ; ; 试题详情
③函数 是偶函数; 是偶函数; 试题详情
④ 是函数 是函数 的一条对称轴方程; 的一条对称轴方程; 试题详情
试题详情
⑥若 ,且 ,且 ,则 ,则 . . 其中正确命题的序号是_______________. 试题详情
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
试题详情
已知函数 . . 试题详情
(1)求 的最小正周期; 的最小正周期; 试题详情
(2)求 的单调递增区间; 的单调递增区间; 试题详情
(3)求 图象的对称轴方程和对称中心的坐标. 图象的对称轴方程和对称中心的坐标. 试题详情
18.(本小题满分12分) 一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正 试题详情
四面体面朝下的数字分别为 ,记 ,记 . . 试题详情
(1)分别求出 取得最大值和最小值时的概率; 取得最大值和最小值时的概率; 试题详情
(2)求 的分布列及数学期望. 的分布列及数学期望. 试题详情
19.(本小题满分12分)如图,多面体 的直观图及三视图如图所示, 的直观图及三视图如图所示, 分别 分别 试题详情
 为 为 的中点. 的中点.
试题详情
(1)求证: 平面 平面 ; ; 试题详情
(2)求多面体 的体积; 的体积; 试题详情
(3)求证: . . 试题详情
试题详情
 . . 试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
(2) 的值. 的值. 试题详情
试题详情
21.(本小题满分13分)已知椭圆
的两焦点与短轴的一个端点的 试题详情
连线构成等腰直角三角形,直线 是抛物线 是抛物线 的一条切线. 的一条切线. (1)求椭圆的方程; 试题详情
(2)过点 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一 个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在, 请说明理由. 试题详情
试题详情
试题详情
 上恒成立. 上恒成立. 试题详情
(1)求 的值; 的值; 试题详情
(2)若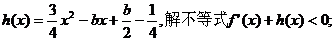 试题详情
(3)是否存在实数m,使函数 上有最小值-5?若 上有最小值-5?若 存在,请求出实数m的值;若不存在,请说明理由. 参
考 答 案 试题详情
一、选择题
试题详情
2.解析: = = ,故选B. ,故选B. 试题详情
| | | |

 若
若 ,
, 等于 ( )
等于 ( ) (
( 是虚数单位)在复平面上对应的点位于 ( )
是虚数单位)在复平面上对应的点位于 ( ) 中,“
中,“ ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件. 中,G是
中,G是 的中点,则
的中点,则 到平面
到平面 的距离是( )
的距离是( ) B.
B. C.
C. D.
D.