
四川省金堂中学高2009级数学模拟试题(1)
第Ⅰ卷(选择题,共60分)
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.已知a>b>0,全集为R,集合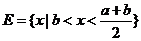 ,
,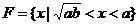 ,
,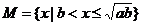 ,则有( )
,则有( )
A. (
(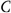
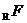 ) B.
) B.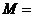 (
(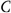
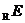 )
)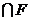 C.
C.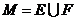 D.
D.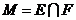
2.已知实数a,b均不为零, ,且
,且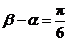 ,则
,则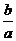 等于( )
等于( )
A.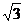 B.
B.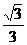 C.
C.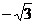 D.
D.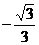
3.已知函数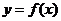 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当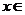 (0,+∞)时,
(0,+∞)时, ,则当
,则当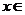 (-∞,-2)时
(-∞,-2)时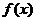 的解析式为( )
的解析式为( )
A.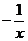 B.
B.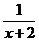 C.
C.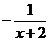 D.
D.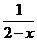
4.已知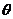 是第三象限角,
是第三象限角,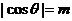 ,且
,且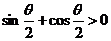 ,则
,则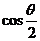 等于( )
等于( )
A.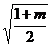 B.
B.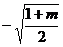 C.
C.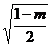 D.
D.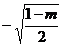
5.(理) 已知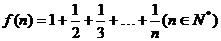 ,用数学归纳法证明
,用数学归纳法证明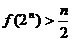 时,
时,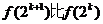 多的项数是
( )
多的项数是
( )
A.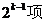 B.
B. 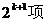 C.
C. 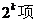 D.
D.
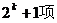
(文)过抛物线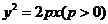 的焦点作直线交抛物线于
的焦点作直线交抛物线于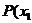 ,
,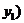 、
、 ,
, 两点,若
两点,若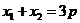 ,则
,则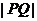 等于( )
等于( )
A.4p B.5p C.6p D.8p
6.设a,b,c是空间三条直线,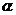 ,
,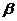 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当c⊥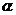 时,若c⊥
时,若c⊥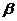 ,则
,则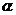 ∥
∥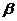 B.当
B.当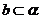 时,若b⊥
时,若b⊥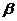 ,则
,则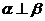
C.当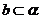 ,且c是a在
,且c是a在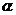 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥b
D.当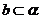 ,且
,且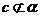 时,若c∥
时,若c∥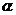 ,则b∥c
,则b∥c
7.两个非零向量a,b互相垂直,给出下列各式:
①a?b=0;
②a+b=a-b; ③|a+b|=|a-b|;
④|a|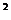 +|b|
+|b|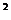 =
=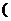 a+b
a+b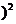 ; ⑤(a+b)?(a-b)=0.其中正确的式子有( )
; ⑤(a+b)?(a-b)=0.其中正确的式子有( )
A.2个 B.3个 C.4个 D.5个
8.已知数列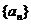 为等差数列,现在
为等差数列,现在 则
则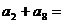 ( )
( )
A.90 B.100 C.180 D.200
9.在含有30个个体的总体中,抽取一个容量为5的样本,则个体a被抽到的概率为( )
A.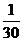 B.
B.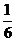 C.
C.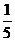 D.
D.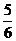
10.过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,则球的表面积是( )
A.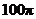 B.
B.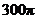 C.
C.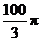 D.
D.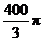
11.(理)某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有( )
A.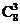 种 B.
种 B.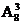 种 C.
种 C.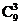 种 D.
种 D.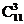 种
种
(文)某师范大学的2名男生和4名女生被分配到两所中学作实习教师,每所中学分配1名男生和2名女生,则不同的分配方法有( )
A.6种 B.8种 C.12种 D.16种
12.已知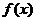 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意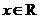 ,都有
,都有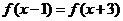 ,当
,当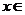 [4,6]时,
[4,6]时,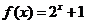 ,则函数
,则函数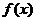 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数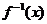 的值
的值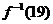 为( )
为( )
A.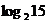 B.
B.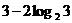 C.
C.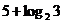 D.
D.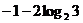
第Ⅱ卷(非选择题,共90分)
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.(文)函数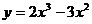 在[0,3]上的最大值为________.
在[0,3]上的最大值为________.
(理)从某社区150户高收入家庭,360户中等收入家庭,90户低收入家庭中,用分层抽样法选出100户调查社会购买力的某项指标,则三种家庭应分别抽取的户数依次为________.
14.若实数a,b均不为零,且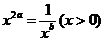 ,则
,则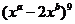 展开式中的常数项等于________.
展开式中的常数项等于________.
15.若数列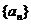 ,
,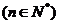 是等差数列,则有数列
是等差数列,则有数列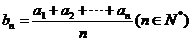 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列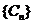 是等比数列,且
是等比数列,且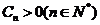 ,则有
,则有 __________
__________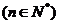 也是等比数列..
也是等比数列..
16.(理)给出下列4个命题:
①函数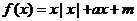 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数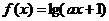 的定义域是
的定义域是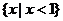 ,则
,则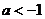 ;
;
③若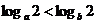 ,则
,则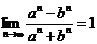 (其中
(其中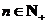 );
);
④圆: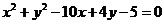 上任意点M关于直线
上任意点M关于直线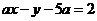 的对称点,
的对称点,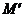 也在该圆上.
也在该圆上.
填上所有正确命题的序号是________.
(文)关于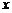 的函数
的函数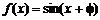 有以下命题:
有以下命题:
(1)对任意的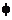 ,
,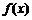 都是非奇非偶函数;
都是非奇非偶函数;
(2)不存在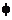 ,使
,使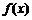 既是奇函数,又是偶函数;
既是奇函数,又是偶函数;
(3)存在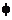 ,使
,使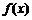 是奇函数;
是奇函数;
(4)对任意的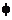 ,
,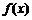 都不是偶函数
都不是偶函数
其中一个假命题的序号是_______ 因为当
因为当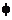 =_______时,该命题的结论不成立
=_______时,该命题的结论不成立
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(12分)已知函数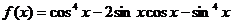
(1)求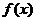 的最小正周期;(2)若
的最小正周期;(2)若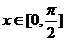 ,求
,求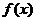 的最大以及最小值
的最大以及最小值
18.(12分)已知二次函数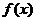 对任意
对任意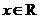 ,都有
,都有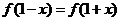 成立,设向量
成立,设向量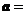 (sinx,2),
(sinx,2),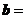 (2sinx,
(2sinx,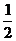 ),
),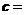 (cos2x,1),
(cos2x,1),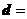 (1,2),当
(1,2),当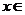 [0,
[0,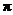 ]时,求不等式f(
]时,求不等式f(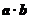 )>f(
)>f(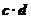 )的解集.
)的解集.
19.(12分)(理)甲、乙队进行篮球总决赛,比赛规则为:七场四胜制,即甲或乙队,谁先累计获胜四场比赛时,该队就是总决赛的冠军,若在每场比赛中,甲队获胜的概率均为0.6,每场比赛必须分出胜负,且每场比赛的胜或负不影响下一场比赛的胜或负.
(1)求甲队在第五场比赛后获得冠军的概率;(2)求甲队获得冠军的概率;
(文)有甲、乙两只口袋,甲袋装有4个白球2个黑球,乙袋装有3个白球和4个黑球,若从甲、乙两袋中各任取出两球后并交换放入袋中.
(1)求甲袋内恰好有2个白球的概率;(2)求甲袋内恰好有4个白球的概率;
20.(12分)长方体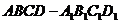 中,
中, ,
,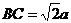 ,M是AD中点,N是
,M是AD中点,N是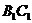 中点.
中点.
(1)求证 :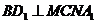 ;(2)求证:平面
;(2)求证:平面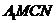 ⊥平面
⊥平面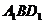 ;
;
(2)求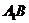 与平面
与平面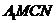 所成的角.
所成的角.
21.(12分)已知椭圆方程为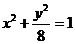 ,射线
,射线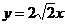 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(1)求证直线AB的斜率为定值;
(2)求△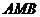 面积的最大值.
面积的最大值.
22.(14分)已知等差数列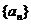 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,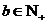 ,且
,且 .
.
(1)求a的值;(2)若对于任意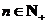 ,总存在
,总存在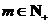 ,使
,使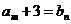 ,求b的值;
,求b的值;
(3)在(2)问中,记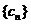 是所有
是所有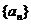 中满足
中满足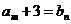 ,
, 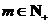 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记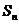 为
为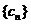 的前n项和,
的前n项和,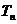
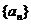 的前n项和,求证:
的前n项和,求证: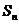 ≥
≥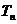
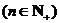 .
.
(文科只做前两问)
一、选择
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A
10.B 11.(理)A (文)C 12.B
二、填空
13.(理) (文)25,60,15 14.-672 15.2.5小时 16.(理)①,④(文)(1),
(文)25,60,15 14.-672 15.2.5小时 16.(理)①,④(文)(1), ;(1),
;(1), ;(4),
;(4), 等
等
三、解答题
17.解析:设f(x)的二次项系数为m,其图象上两点为(1-x, )、B(1+x,
)、B(1+x, )因为
)因为 ,
, ,所以
,所以 ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵  ,
, ,
, ,
, ,
, ,
,
 ,
,
∴ 当 时,
时,




 ,
, .
.
∵  , ∴
, ∴  .
.
当 时,同理可得
时,同理可得 或
或 .
.
综上: 的解集是当
的解集是当 时,为
时,为 ;
;
当 时,为
时,为 ,或
,或 .
.
18.解析:(理)(1)设甲队在第五场比赛后获得冠军为事件M,则第五场比赛甲队获胜,前四场比赛甲队获胜三场
依题意得 .
.
(2)设甲队获得冠军为事件E,则E包含第四、第五、第六、第七场获得冠军四种情况,且它们被彼此互斥.
∴  .
.
(文)①设甲袋中恰有两个白球为事件A

②设甲袋内恰好有4个白球为事件B,则B包含三种情况.
甲袋中取2个白球,且乙袋中取2个白球,②甲袋中取1个白球,1个黑球,且乙袋中取1个白球,1个黑球,③甲、乙两袋中各取2个黑球.
∴ 
 .
.
19.解析:(1)取 中点E,连结ME、
中点E,连结ME、 ,
,
∴ 

 ,MC
,MC EC. ∴
EC. ∴ 
 MC. ∴
MC. ∴  ,M,C,N四点共面.
,M,C,N四点共面.

(2)连结BD,则BD是 在平面ABCD内的射影.
在平面ABCD内的射影.
∵  , ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
, ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
∴ ∠CBD+∠BCM=90°. ∴ MC⊥BD. ∴  .
.
(3)连结 ,由
,由 是正方形,知
是正方形,知 ⊥
⊥ .
.
∵  ⊥MC, ∴
⊥MC, ∴  ⊥平面
⊥平面 .
.
∴ 平面 ⊥平面
⊥平面 .
.
(4)∠ 是
是 与平面
与平面 所成的角且等于45°.
所成的角且等于45°.
20.解析:(1) .
.
∵ x≥1. ∴  ,
,
当x≥1时, 是增函数,其最小值为
是增函数,其最小值为 .
.
∴ a<0(a=0时也符合题意). ∴ a≤0.
(2) ,即27-6a-3=0, ∴ a=4.
,即27-6a-3=0, ∴ a=4.
∴  有极大值点
有极大值点 ,极小值点
,极小值点 .
.
此时f(x)在 ,
, 上时减函数,在
上时减函数,在 ,+
,+ 上是增函数.
上是增函数.
∴ f(x)在 ,
, 上的最小值是
上的最小值是 ,最大值是
,最大值是 ,(因
,(因 ).
).
21.解析:(1)∵ 斜率k存在,不妨设k>0,求出M( ,2).直线MA方程为
,2).直线MA方程为 ,直线MB方程为
,直线MB方程为 .
.
分别与椭圆方程联立,可解出 ,
, .
.
∴  . ∴
. ∴  (定值).
(定值).
(2)设直线AB方程为 ,与
,与 联立,消去y得
联立,消去y得
 .
.
由D>0得-4<m<4,且m≠0,点M到AB的距离为 .
.
设△AMB的面积为S. ∴  .
.
当 时,得
时,得 .
.
22.解析:(1)∵  ,a,
,a, ,
,
∴  ∴
∴  ∴
∴ 
∴  .
.
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
(2) ,
, ,由
,由 可得
可得
 . ∴
. ∴  .
.
∴ b=5
(3)由(2)知 ,
, , ∴
, ∴  .
.
∴  . ∴
. ∴  ,
, .
.
∵  ,
, .
.
当n≥3时,



 .
.
∴  . 综上得
. 综上得 
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com