
崇文区2008―2009学年度第二学期高三统一练习(一)
数 学(文科) 2009.3
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟,考试结束,将本试卷和答题卡一并交回。
第I卷(选择题 共40分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。不能答在试卷上。
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合
A. B.
B. C.
C. D.
D.
2.抛物线 的焦点坐标是
的焦点坐标是
A. B.
B. C.
C. D.
D.
3.已知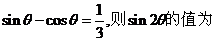
A. B.
B. C.
C. D.
D.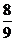
4.设 是公差为-2的等差数列,如果
是公差为-2的等差数列,如果 则
则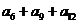 =
=
A.40 B.30 C.20 D.10
5.下列命题中,正确的命题是
A.过空间任一点P均存在着与平面 平行的直线
平行的直线
B.过空间任一点P均存在着与平面 垂直的直线
垂直的直线
C.过空间任一点P均存在着与平面 平行的无数多条直线
平行的无数多条直线
D.过空间任一点P均存在着与平面 垂直的无数多条直线
垂直的无数多条直线
6.定义在 上的函数
上的函数 是偶函数,且
是偶函数,且 若
若 在区间
在区间 上是增函数,则
上是增函数,则
A.在区间[-2,-1]上是增函数,在区间[5,6]上是增函数
B.在区间[-2,-1]上是增函数,在区间[5,6]上是减函数
C.在区间[-2,-1]上是减函数,在区间[5,6]上是增函数
D.在区间[-2,-1]上是减函数,在区间[5,6]上是减函数
 7.在如图所示的坐标平面的可行域内(阴影部分且包括边
7.在如图所示的坐标平面的可行域内(阴影部分且包括边
界),若目标函数 取得最小值的最优解有无数
取得最小值的最优解有无数
个则 等于
等于
A.1 B.-1
C.3 D.-3
8.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数 的图象恰好通过
的图象恰好通过 个格点,则称函数
个格点,则称函数 为
为 阶格点函数,下列函数:
阶格点函数,下列函数:
① ; ②
; ② ; ③
; ③ ; ④
; ④
其中一阶格点函数的有
A.①② B.①④ C.①②④ D.①②③④
二、填空题:本大题共6个小题,每小题5分,共30分。把答案填在题中横线上。
9.已知 展开式的第二项与第三项的系数比是1:2,则
展开式的第二项与第三项的系数比是1:2,则 =_____________。
=_____________。
10.若把函数 的图象按向量
的图象按向量 平移,得到函数
平移,得到函数 的图象,则向量
的图象,则向量 的坐标为______________。
的坐标为______________。
11.某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排,其中甲、乙两种必须排在一起,而丙、乙两种不能排在一起,不同的排法共有_________种(用数字做答)
 12.如图,等腰梯形
12.如图,等腰梯形 中,
中, 分别上一
分别上一 边上的三等分点,
边上的三等分点, 若三角形
若三角形 和
和 分别沿
分别沿 和
和 折起,使得
折起,使得 两点重合于一点
两点重合于一点 、则二面角
、则二面角 的大小为_________。
的大小为_________。
13.已知点 为椭圆
为椭圆 上的动点,
上的动点, ,
, 为椭圆的左,右焦点,则
为椭圆的左,右焦点,则 的最小值为_________,此时
的最小值为_________,此时 点的坐标为____________________。
点的坐标为____________________。
14.对于集合 的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合
的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合 的交替和是9-6+4-2+1=6,集合
的交替和是9-6+4-2+1=6,集合 的交替和为5,当集合
的交替和为5,当集合 中的
中的 时,集合
时,集合 的所有非空子集为
的所有非空子集为 ,则它的“交替和”的总和
,则它的“交替和”的总和 ,则当时
,则当时 =______________;根据
=______________;根据 ,猜想集合
,猜想集合 的每一个非空子集的“交替和”的总和
的每一个非空子集的“交替和”的总和 __________。
__________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分13分)
在 中,角
中,角 所对的边分别为
所对的边分别为 ,向量
,向量
 ,且
,且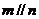
(I)求 的大小;
的大小;
(Ⅱ)求 的值。
的值。
16.(本小题满分14分)
已知直四棱柱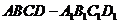 中,
中, ,
,
(I)求证: ;
;
(Ⅱ)求 与平面
与平面 所成角的大小
所成角的大小

17.(本小题满分13分)
已知函数 。
。
(I)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)当 时,讨论函数
时,讨论函数 的单调性。
的单调性。
18.(本小题满分13分)
 某学校进行交通安全教育,设计了如下游戏,如图,一辆车模要直行通过十字路口,此时前方交通灯为红灯,且该车模前面已有4辆车模依次在同一车道上排队等候(该车道只可以直行或左转行驶),已知每辆车模直行的概率是
某学校进行交通安全教育,设计了如下游戏,如图,一辆车模要直行通过十字路口,此时前方交通灯为红灯,且该车模前面已有4辆车模依次在同一车道上排队等候(该车道只可以直行或左转行驶),已知每辆车模直行的概率是 ,左转行驶的概率是
,左转行驶的概率是 ,该路口红绿灯转换间隔时间均为1分钟,假设该车道上一辆直行去东向的车模驶出停车线需要10秒钟,一辆左转去北向的车模驶出停车线需要20秒种,求:
,该路口红绿灯转换间隔时间均为1分钟,假设该车道上一辆直行去东向的车模驶出停车线需要10秒钟,一辆左转去北向的车模驶出停车线需要20秒种,求:
(I)前4辆车模中恰有2辆车左转行驶的概率;
(Ⅱ)该车模在第一次绿灯量起时的1分钟内通过该
路口概率(汽车驶出停车线就算通过路口)
19.(本小题满分14分)
已知 ,
, ,动点
,动点 满足
满足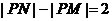 ,点
,点 的轨迹为
的轨迹为 ,过点
,过点 的直线为轨迹
的直线为轨迹 交于
交于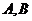 两点
两点
(I)求轨迹 的方程;
的方程;
(Ⅱ)若 ,求直线
,求直线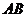 斜率
斜率 的值,并判断以线段
的值,并判断以线段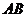 为直径的圆与直线
为直径的圆与直线 的位置关系并说明理由
的位置关系并说明理由
20.(本小题满分13分)
已知函数 ,数列
,数列 满足条件:
满足条件:

 。
。
(I)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 ,并求使得
,并求使得 对任意
对任意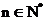 都成立的最大正整数
都成立的最大正整数 ;
;
(Ⅲ)求证:




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com