
2005年天津市高级中等学校招生考试.
第Ⅰ卷
一、 选择题:本大题共10小题,每小题3分,共30分.在每小题给出的4个选项中,只有1项是符合题目要求的.
(A)
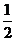 (B)
(B)
(C) (D)
1
(D)
1
(2) 不等式组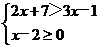 的解集为
的解集为
(A)2<x<8 (B) 2≤x<8
(C) x<8 (D) x≥2
(3) 如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于
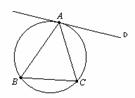
(A)30° (B)60° (C)90° (D)120°
(4) 下列命题中的真命题是
(A)关于中心对称的两个图形全等
(B) 全等的两个图形是中心对称图形
(C) 中心对称图形都是轴对称图形
(D) 轴对称图形都是中心对称图
(5) 如图,在 ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有
ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有
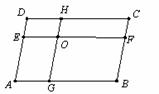
(A)7 个 (B)8个
(C)9个 (D)11个
 (6)
已知甲、乙两组数据的平均数相等,若甲组数据的方差
(6)
已知甲、乙两组数据的平均数相等,若甲组数据的方差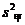 =0.055,乙组数据的方差
=0.055,乙组数据的方差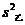 =0.105,则
=0.105,则
(A)甲组数据比乙组数据波动大 (B)乙组数据比甲组数据波动大
(C)甲组数据与乙组数据的波动一样大 (D)甲、乙两组数据的数据波动不能比较
(7) 如果限定用一种正多边形镶嵌,在下面的正多边形中,不能镶嵌成一个平面的是
(A)正三角形 (B)正方形
(C)正五边形 (D) 正六边形
(8) 在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是
(A)AC=BD,AB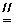 CD
CD
(B) AD//BC,∠A=∠C
(C) AO=BO=CO=DO,AC⊥BD
(D)AO=CO,BO=DO,AB=BC
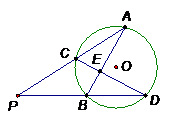
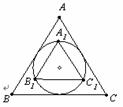
(9) 如图,若正△A1B1C1内接于正△ABC的内切圆,则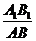 的值为
的值为
(A)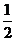 (B)
(B) (C)
(C) 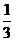 (D)
(D)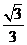
(10) 若关于x的一元二次方程2x2-2x+3m-1=0的两个实数根x1,x2,且x1?x2>x1+x2-4,则实数m的取值范围是
(A)m>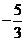 (B)
m≤
(B)
m≤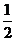 (C) m<
(C) m<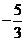 (D)
(D) 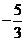 <m≤
<m≤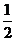
第Ⅱ卷
二、填空题:本大题共8小题,每小题3分,共24分.请将答案直接填在题中横线上.
(11)已知|x|=4,|y|=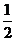 ,且xy<0,则
,且xy<0,则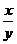 的值等于
.
的值等于
.
(12)若a=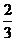 ,
,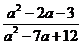 的值等于________.
的值等于________.
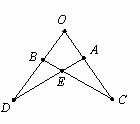
(13) 如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED等于___________(度)
(14) 如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于____________(度)

(15) 已知一组数据:-2,-2,3,-2,x,-1,若这组数据的平均数是0.5,则这组数据的中位数是______________
(16) 若正比例函数y =kx与y=2x的图像关于x轴对称,则k的等于___________
(17) 如图,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于______________cm
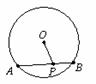
(18)如图,已知五边形ABCDE中,AB//ED,∠A=∠B=90°,则可以将该五边形ABCDE分成面积相等的两部分的直线有__________条,满足条件的直线可以这样趋确定:
_______________________________________________________________
____________________________________________________
(19)(本小题6分)
三、解答题:本大题共8小题,共66分。解答应写出文字说明、演算步骤或证明过程.
解方程组 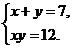
(20)(本小题8分)
已知关于x的一次函数y=kx+1和反比例函数y=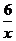 的图像都经过点(2,m)。
的图像都经过点(2,m)。
(Ⅰ)求一次函数的解析式;
(Ⅱ)求这两个函数图像的另一个交点的坐标。
(21)(本小题8分)
已知抛物线y=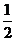 x2+x-
x2+x-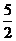 .
.
(Ⅰ)用配方法求出它的顶点坐标和对称轴;
(Ⅱ)若抛物线与x轴的两个交点为A、B,求线段AB的长.
(22)(.本小题8分)
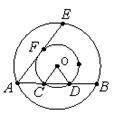
如图,在以O为圆心的两个同心圆中,小圆的半径长为2,大圆的弦AB与小圆交于点C、D,且∠COD=60°。
(Ⅰ)求大圆半径的长;
(Ⅱ)若大圆的弦AE与小圆切于点F,求AE的长.
(23)(本小题8分)
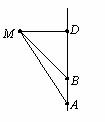
如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?(精确到0.1海里,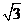 ≈1.732)
≈1.732)
(24)(本小题8分)
注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答;也可以选用其他的解题方案,此时不必填空,,只需按照解答题的一般要求,进行解答。
李明计划在一定日期内读完200页的一本书,读了5天后改变了计划,每天多读5页,结果提前一天读完,求他原计划平均每天读几页书。
解题方案:设李明原计划平均每天读书x页,用含x的代数式表示:
(Ⅰ)李明原计划读完这本书需用______________天;
(Ⅱ)改变计划时,已读了______________页,还剩______________页;
(Ⅲ)读了5天后,每天多读5页,读完剩余部分还需________________天;
(Ⅳ)根据问题中的相等关系,列出相应方程_________________________________;
(Ⅴ)李明原计划平均每天读书___________页(用数字作答)
(25)(本小题10分)
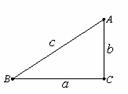
在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
(Ⅰ)如图,在△ABC中,∠A=2∠B,且∠A=60°。求证:a2=b(b+c)
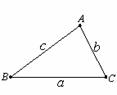
(Ⅱ)如果一个三角形的一个内角等于另一个内角的2 倍,我们称这样的三角形为“倍角三角形”。本题第一问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成了?并证明你的结论;
(Ⅲ)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数。
(26) (本小题10分)
已知二次函数y=ax2+bx+c.
(Ⅰ)若a=2,c=-3,且二次函数的图像经过点(-1,-2),求b的值
(Ⅱ)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p,-2),求证:b≥0;
(Ⅲ)若a+b+c=0,a>b>c,且二次函数的图像经过点(q,-a),试问自变量x=q+4时,二次函数y=ax2+bx+c所对应的函数值y是否大于0?并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com