9．不等式组

       A．x＜ ? 2          B．? 2＜x≤            

C．? 2＜x≤1        D．x＜? 2或x≥1

10．如图，在    ABCD中，EF∥AB，DE∶EA = 2∶3，EF = 4，则CD的长为（    ）

       A．        B．8          C．10         D．16

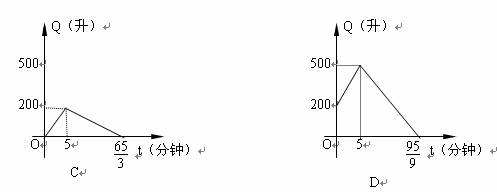
11．有一个装有进、出水管的容器，单位时间年7进、出的水量都是一定的。已知容器的容积为600升，又知单开进水管10分钟可把空容器注满，若同时打开进、出水管，20分钟可把满容器的水放完，现已知水池内有水200升，先打开进水管5分钟后，再打开出水管，两管同时开放，直至把容器中的水放完，则能正确反映这一过程中容器的水量Q（升）随时间t（分）变化的图像是（    ）

                                      第二卷

12．（本题满分7分）

如图，在Rt△ABC中，∠ACB = 90°，∠BAC = 60°，DE垂直平分BC，垂足为D，交AB于点E。又点F在DE的延长线上，且AF = CE。求证：四边形ACEF是菱形。

13．（本题满分7分）

张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为15米³的无盖长方体运输箱，且此长方体运输箱底面的长比宽多2米，现已知购买这种铁皮每平方米需20元，问张大叔购回这张矩形铁皮共花了多少元钱？

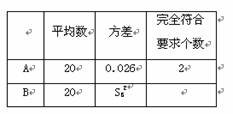
14．（本题满分7分）

为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm）

根据测试得到的有关数据，试解答下列问题：

⑴ 考虑平均数与完全符合要求的个数，你认为           的成绩好些；

⑵ 计算出S_B²的大小，考虑平均数与方差，说明谁的成绩好些；

⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由。

          1  2 3 4  5  6 7 8  9 10 件数

15．下列关于一元二次方程的四种说法，你认为正确的是（       ）

A．  方程2y ² ? y + = 0必有实数根；       

B．  方程? x ² + x + 1 = 0的两个实数根之积为? 1；

C．  以? 1、2两数为根的一元二次方程可记为：x ² + x ? 2 = 0

D．  一元二次方程2x ² + 4x + 3m = 0的两实数根的平方和为7，则m = ? 1；

16．如图，△ABC中，AB = AC，D为BC中点，E为AD上任意一点，过C作CF∥AB交BE的延长线于F，交AC于G，连结CE。下列结论中正确的有（       ）

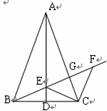A．AD平分∠BAC    B．BE = CF           C．BE = CE          

D. 若BE = 5，GE = 4，则GF =

五、解答下列问题

     饮水问题是关系到学生身心健康的重要生活环节，东坡中学共有教学班24个，平均每班有学生50人，经估算，学生一年在校时间约为240天（除去各种节假日），春、夏、秋、冬季各60天。原来，学生饮水一般都是购纯净水（其它碳酸饮料或果汁价格更高），纯净水零售价为1.5元 / 瓶，每个学生春、秋、冬季平均每天买1瓶纯净水，夏季平均每天要买2瓶纯净水，学校为了减轻学生消费负担，要求每个班自行购买1台冷热饮水机，经调查，购买一台功率为500w的冷热饮水机约为150元，纯净水每桶6元，每班春、秋两季，平均每1.5天购买4桶，夏季平均每天购买5桶，冬季平均每天购买1桶，饮水机每天开10小时，当地民用电价为0.50元 / 度。

问题：

⑴ 在未购买饮水机之前，全年平均每个学生要花费          元钱来购买纯净水饮用？

⑵ 请计算：在购买饮水机解决学生饮水问题后，每班当年共要花费多少元？

⑶ 这项便利学生的措施实施后，东坡中学一年要为全体学生共节约         元钱？

18．（本题满分10分）

如图，已知⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA = EC。

⑴ 求证：AC ² = AE?AB；

⑵ 延长EC到点P，连结PB，若PB = PE，试判断PB与⊙O的位置关系，并说明理由。

19．（本题满分9分）

宏远广告公司要为某企业的一种产品设计商标图案，给出了如下几种初步方案，供继续设计选用（设图中圆的半径均为r）

⑴ 如图1，分别以线段O₁O₂的两个端点为圆心，以这条线段的长为半径作出两个互相交错的圆的图案，试求两圆相交部分的面积；

⑵ 如图2，分别以等边△O₁O₂O₃的三个顶点为圆心，以其边长为半径，作出三个两两相交的相同的圆，这时，这三个圆相交部分的面积又是多少呢？

⑶ 如图3，分别以正方形O₁O₂O₃O₄的四个顶点为圆心，以其边长为半径，作出四个相同的圆，这时，这四个圆相交部分的面积又是多少呢？

20．（本题满分10分）

在黄州服装批发市场，某种品牌的时装当季节即将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周（7天）涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售。

⑴ 试建立销售价y与周次x之间的函数关系式；

⑵ 若这种时装每件进价Z与周次x之间的关系式为：Z = ? 0.125（x ? 8）² + 12，1≤x≤16，且x为整数，试问该服装第几周出售时，每件销售利润最大？最大利润是多少？

21．（本题满分16分）

如图，在直角坐标系中，O是原点，A、B、C三点的坐标分别为A（18，0），B（18，6），C（8，6），四边形OABC是梯形，点P、Q同时从原点出发，分别坐匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC、CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动。

⑴ 求出直线OC的解析式及经过O、A、C三点的抛物线的解析式。

⑵ 试在⑴中的抛物线上找一点D，使得以O、A、D为顶点的三角形与△AOC全等，

请直接写出点D的坐标。

⑶ 设从出发起，运动了t秒。如果点Q的速度为每秒2个单位，试写出点Q的坐标，

并写出此时t的取值范围。

⑷ 设从出发起，运动了t秒。当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半，这时，直线PQ能否把梯形的面积也分成相等的两部分，如有可能，请求出t的值；如不可能，请说明理由。