
湖北省十堰市2006年课改实验区初中毕业生学业考试
数 学 试 题
第一卷
一、精心选一选(本大题共10小题,每小题都给出代号为A,B,C,D的四个选项,其中有且只有一个选项符合题目要求,把符合题目要求的选项的字母代号直接填在答题框内相应的题号下的方框中,不填、填错或一个方框内填写的代号超过一个,一律得0分;每小题3分,满分30分)
1.下列各式中,一定成立的是( )
A.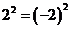 B.
B.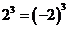
C.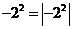 D.
D.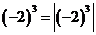
2.二元一次方程组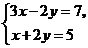 的解是( )
的解是( )
A.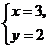 B.
B.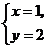
C.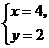 D.
D.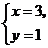
3.下列命题正确的是( )
A.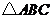 中,如果
中,如果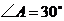 ,那么
,那么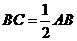 ;
;
B.如果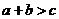 ,那么线段
,那么线段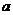 ,
,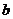 ,
,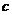 一定可以围成一个三角形;
一定可以围成一个三角形;
C.三角形三边垂直平分线的交点有可能在一边上;
D.平分弦的直径垂直于弦
4.下列四个数据,精确的是( )
A.小莉班上有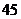 人;
人;
B.某次地震中,伤亡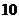 万人;
万人;
C.小明测得数学书的长度为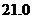 厘米;
厘米;
D.吐鲁番盆地低于海平面大约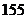 米
米
5.观察图甲,从左侧正对长方体看到的结果是图乙中的( )

6.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用一幅图近似地刻画,这幅图是下图中的( )

7.如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )
A.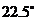 角 B.
角 B.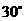 角
C.
角
C.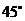 角 D.
角 D.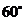 角
角
7题图 8题图 9题图
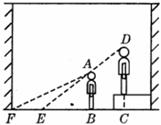
8.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.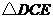 B.四边形
B.四边形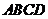
C.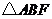 D.
D.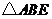
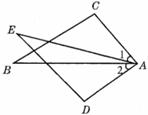
9.如图,已知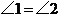 ,
,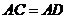 ,增加下列条件:①
,增加下列条件:①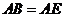 ;②
;②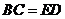 ;③
;③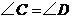 ;④
;④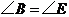 .其中能使
.其中能使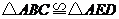 的条件有( )
的条件有( )
A.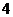 个 B.
个 B.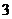 个 C.
个 C.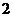 个 D.
个 D.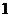 个
个
10.在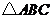 中,
中,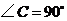 ,
,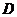 是边
是边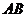 上一点(不与点
上一点(不与点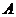 ,
,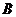 重合),过点
重合),过点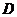 作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有( )
作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有( )
A.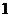 条 B.
条 B.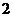 条 C.
条 C.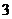 条 D.
条 D.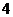 条
条
第二卷
11.已知直线 经过第一、二、四象限,则其解析式可以为______________(写出一个即可).
经过第一、二、四象限,则其解析式可以为______________(写出一个即可).
12.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第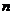 个图形需____________根火柴棒.
个图形需____________根火柴棒.

13.学生小颖自制一个无底圆锥形纸帽,圆锥底面圆的半径为 ,母线长为
,母线长为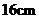 ,那么围成这个纸帽的面积(不计接缝)是_________
,那么围成这个纸帽的面积(不计接缝)是_________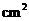 (结果保留三个有效数字).
(结果保留三个有效数字).
14.如图,已知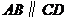 ,
,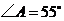 ,
,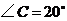 ,则
,则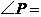 ___________.
___________.
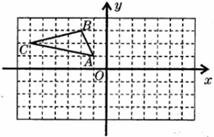
14题图 15题图
15.如图,在平面直角坐标系中,请按下列要求分别作出 变换后的图形(图中每个小正方形的边长为
变换后的图形(图中每个小正方形的边长为 个单位):
个单位):
(1)向右平移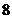 个单位;(2)关于
个单位;(2)关于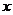 轴对称;(3)绕点
轴对称;(3)绕点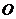 顺时针方向旋转
顺时针方向旋转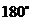 .
.
16.小亮调查本班同学的身高后,将数据绘制成如下图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值.比如,第二小组数据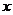 满足:
满足: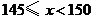 ,其它小组的数据类似).设班上学生身高的平均数为
,其它小组的数据类似).设班上学生身高的平均数为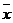 ,则
,则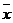 的取值范围是___________________.
的取值范围是___________________.

三、细心做一做(本大题共3小题,满分18分)
17.(5分)计算: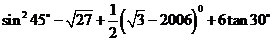 <至少要有两步运算过程).
<至少要有两步运算过程).
18.(5分)化简: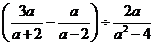 .
.
19.(8分)小莉和小慧用如图所示的两个转盘做游戏,转动两个转盘各一次,若两次数字和为奇数,则小莉胜;若两次数字和为偶数,则小慧胜.这个游戏对双方公平吗?试用列表法或树状图加以分析.
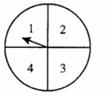

四、静心试一试(本大题共4小题,满分24分)
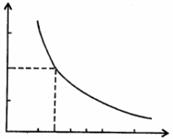
20.(6分)某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强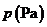 是木板面积
是木板面积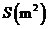 的反比例函数,其图像如下图所示.
的反比例函数,其图像如下图所示.
(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为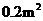 时,压强是多少?
时,压强是多少?
(3)如果要求压强不超过 ,木板的面积至少要多大?
,木板的面积至少要多大?
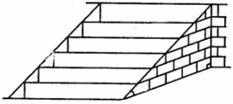
21.(6分)武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由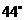 减至
减至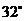 ,已知原台阶
,已知原台阶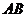 的长为
的长为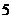 米(
米(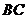 所在地面为水平面).
所在地面为水平面).
(1)改善后的台阶会加长多少?(精确到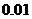 米)
米)
(2)改善后的台阶多占多长一段地面?(精确到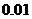 米)
米)
22.(6分)市“康智”牛奶乳业有限公司经过市场调研,决定从明年起对甲、乙两种产品实行“限产压库”,要求这两种产品全年共新增产量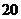 件,这
件,这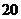 件的总产值
件的总产值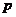 (万元)满足:
(万元)满足: .已知有关数据如下表所示,那么该公司明年应怎样安排新增产品的产量?
.已知有关数据如下表所示,那么该公司明年应怎样安排新增产品的产量?
产品
每件产品的产值
甲
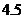 万元
万元
乙
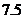 万元
万元
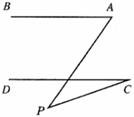
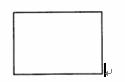
23.(6分)如图甲,李叔叔想要检测雕塑底座正面四边形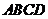 是否为矩形,但他随身只带了有刻度的卷尺,请你设计一种方案,帮助李叔叔检测四边形
是否为矩形,但他随身只带了有刻度的卷尺,请你设计一种方案,帮助李叔叔检测四边形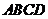 是否为矩形(图乙供设计备用).
是否为矩形(图乙供设计备用).

五、用心想一想(本大题共2小题,满分18分)
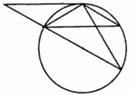
24.(8分)如图, 为
为 的直径,
的直径,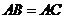 ,
,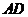 交
交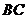 于
于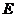 ,
,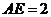 ,
, .
.
(1)求证: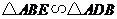 ,并求
,并求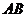 的长;
的长;
(2)延长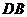 到
到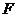 ,使
,使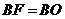 ,连接
,连接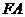 ,那么直线
,那么直线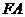 与
与 相切吗?为什么?
相切吗?为什么?
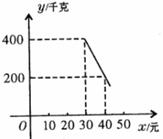
25.(10分)市“健益”超市购进一批 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以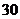 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出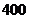 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量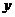 (千克)与销售单价
(千克)与销售单价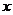 (元)(
(元)( )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出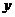 与
与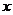 的函数关系式;
的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润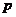 元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过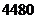 元,现该超市经理要求每天利润不得低于
元,现该超市经理要求每天利润不得低于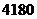 元,请你帮助该超市确定绿色食品销售单价
元,请你帮助该超市确定绿色食品销售单价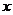 的范围(直接写出).
的范围(直接写出).
六、综合运用(本题满分12分)
26.已知抛物线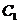 :
: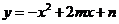 (
( ,
,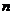 为常数,且
为常数,且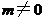 ,
,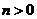 )的顶点为
)的顶点为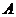 ,与
,与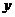 轴交于点
轴交于点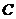 ;抛物线
;抛物线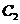 与抛物线
与抛物线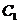 关于
关于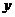 轴对称,其顶点为
轴对称,其顶点为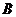 ,连接
,连接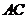 ,
,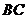 ,
,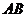 .
.
注:抛物线 的顶点坐标为
的顶点坐标为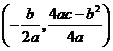 .
.
(1)请在横线上直接写出抛物线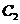 的解析式:________________________;
的解析式:________________________;
(2)当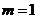 时,判定
时,判定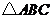 的形状,并说明理由;
的形状,并说明理由;
(3)抛物线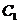 上是否存在点
上是否存在点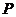 ,使得四边形
,使得四边形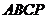 为菱形?如果存在,请求出
为菱形?如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com