
2005年山东省中等学校招生考试(课程改革实验区)
第I卷
一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若a与2互为相反数,则|a+2|等于( )
A. 0 B. -2 C. 2 D. 4
2. 利用因式分解简便计算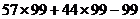 正确的是( )
正确的是( )
A. 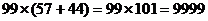
B. 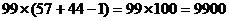
C. 
D. 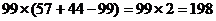
3. 冰柜里装有四种饮料:5瓶特种可乐、12瓶普通可乐、9瓶橘子水、6瓶啤酒,其中特种可乐和普通可乐是含有咖啡因的饮料,那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率是( )
A. 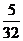 B.
B.
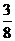 C.
C.
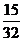 D.
D.
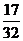
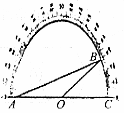
4. 如图,把一个量角器放置在∠BAC的上面,请你根据量角器的读数判断∠BAC的度数是( )
A. 30° B. 60° C. 15° D. 20°

5. 如图,表示某校一位初三学生平时一天的作息时间安排,临近中考他又调整了自己的作息时间,准备再放弃1个小时的睡觉时间、原运动时间的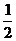 和其他活动时间的
和其他活动时间的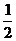 ,全部用于在家学习,那么现在他用于在家学习的时间是( )
,全部用于在家学习,那么现在他用于在家学习的时间是( )

A. 3.5小时 B. 4.5小时 C. 5.5小时 D. 6小时
6. 如图,是在同一坐标系内做出的一次函数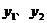 的图像
的图像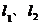 ,设
,设 ,
, ,则方程组
,则方程组 的解是( )
的解是( )
A. 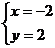 B.
B.
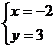
C. 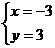 D.
D.
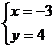
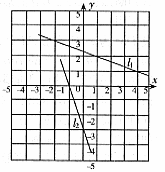
7. 在正方体的表面上画有如图(1)中所示的粗线,图(2)是其展开图的示意图,但只在A面上画有粗线,那么将图(1)中剩余两个面中的粗线画入图(2)中,画法正确的是(如果没把握,还可以动手试一试噢!)( )

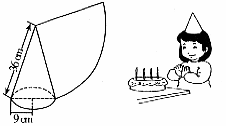
8. 小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形生日礼帽。如图,圆锥帽底面半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为( )
A. 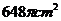 B.
B.
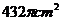 C.
C.
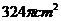 D.
D.
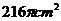
9. 如图,用不同颜色的马赛克片覆盖一个圆形的台面,估计15°圆心角的扇形部分大约需要34片马赛克片。已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面
A. 5~6箱 B. 6~7箱 C. 7~8箱 D. 8~9箱

10. 如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从O3走到正方形O3KJP的中心O4,一共走了 ,则长方形花坛ABCD的周长是( )
,则长方形花坛ABCD的周长是( )
A. 36m B. 48m C. 96m D. 60m

第II卷
二、填空题:本大题共6小题,每小题3分,共18分,把答案填写在题中横线上。
11. “太阳能”是一种既无污染又节省地下能源的能量,据科学家统计,平均每平方千米的地面一年从太阳中获得的能量,相当于燃烧130000000千克的煤所产生的能量,用科学记数法表示这个数量是__________千克。
12. 如图所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形。将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑茹形(取出的一张纸片画有半圆、一张纸片画有正方形)则乙方赢。你认为这个游戏对双方是公平的吗?若不是,有利于谁?__________________________________________________。

13. 某商场计划每月销售900台电脑,5月1日至7日黄金周期间,商场决定开展促销活动,5月的销售计划又增加了30%。已知黄金周这7天平均每天销售54台,则这个商场本月后24天平均每天至少销售__________台才能完成本月计划。
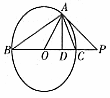
14. 如图,点P是圆O的直径BC的延长线上一点,过点P作圆O的切线PA,切点为A,连结BA、OA、CA,过点A作AD⊥BC于D,请你找出图中共有__________个直角(不要再添加辅助线),并用“┓”符号在图中标注出来。
15. 如图(1),将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为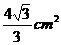 ,则这个旋转角度为__________度。如图(2),将上述两个互相重合的正方形纸片沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动,若重叠部分△A’PC的面积是1cm2,则它移动的距离AA’等于__________cm。
,则这个旋转角度为__________度。如图(2),将上述两个互相重合的正方形纸片沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动,若重叠部分△A’PC的面积是1cm2,则它移动的距离AA’等于__________cm。
16. 把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行……,中间用虚线围的一列,从上至下依次为1、5、13、25、…,则第10个数为__________。

三、解答题:本大题共11小题,共72分,解答应写出文字说明或演算步骤。
17. (本题6分)解一元二次方程: 。
。
18. (本题6分)当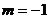 时,求
时,求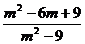 的值。
的值。
19. (本题7分)某区在改革学生学习方式的研究中,对某校七年级的600名学生进行了“你喜欢什么样的学习方式”的问卷调查(如下表),调查者根据统计的数据制作了如下统计图。请你根据图中的有关信息回答下列问题:
(1)请将每种学习方式中选择“最喜欢”的人数填入下表:
代号
选择“最喜欢”的人数
1
2
3
4
5
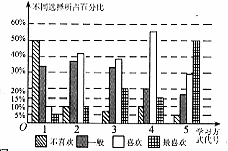
(2)根据图中的信息,请你提出一个问题。
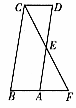
20. (本题7分)如图,已知平行四边形ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F。
(1)求证:CD=FA;
(2)若使∠F=∠BCF,平行四边形ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并进行证明(不要再增添辅助线)。
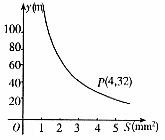
21. (本题6分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)s(mm2)的反比例函数,其图像如图所示。
(1)写出y与S的函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少米?
22. (本题6分)如图,某种旅行帽的帽沿接有两个塑料帽带,其中一个塑料帽带上有7个等距的小圆柱体扣,另一个帽带上扎有七个等距的扣眼,下表列出的是用第一扣分别去扣不同扣眼所测得帽圈直径的有关数据(单位:cm):
扣眼号数(x)
1
2
3
4
5
6
7
帽圈直径(y)
22.92
22.60
22.28
21.96
21.64
21.32
21.00


(1)求帽圈直径y与扣眼号数x之间的一次函数关系式;
(2)小强的头围约为68.94cm,他将第一扣扣到第4号扣眼,你认为松紧合适吗?
23. (本题7分)如图,A、B、C表示建筑在一座比较险峻的名山上的三个缆车站的位置,AB、BC表示连接三个缆车站的钢缆。已知A、B、C所处位置的海拔高度分别为124m、400m、1000m,如图建立直角坐标系,即A(a,124)、B(b,400),C(c,1100),若直线AB的解析式为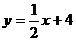 ,直线BC与水平线BC1的交角为45°。
,直线BC与水平线BC1的交角为45°。
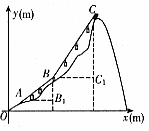
(1)分别求出A、B、C三个缆车站所在位置的坐标;
(2)求缆车从B站出发到达C站单向运行的距离。(精确到1m)
24. (本题6分)如图,在一个长40m、宽30m的长方形小操场上,王刚从A点出发,沿着A→B→C的路线以3m/s的速度跑向C地。当他出发4s后,张华有东西需要交给他,就从A地出发沿王刚走的路线追赶。当张华跑到距B地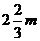 的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上。此时,A处一根电线杆在阳光下的影子也恰好落在对角线AC上。
的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上。此时,A处一根电线杆在阳光下的影子也恰好落在对角线AC上。
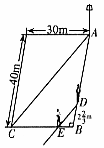
(1)求他们的影子重叠时,两人相距多少米(DE的长)?
(2)求张华追赶王刚的速度是多少(精确到0.1m/s)?
25. (本题6分)小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢?”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次。铅球推出后沿抛物线形运动。如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
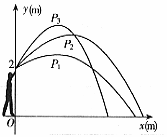
推铅球的方向与 水平线的夹角
30°
45°
60°
铅球运行所得到 的抛物线解析式


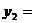 ___________
___________ 
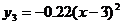
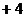
估测铅球在 最高点的坐标
P1(3,2.5)
P2(4,3.6)
P3(3,4)
铅球落点到小明站 立处的水平距离
9.5m
________m
7.3m
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议。
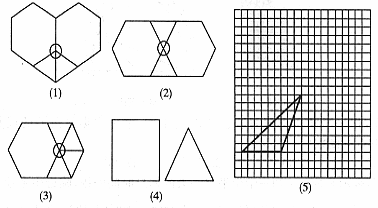
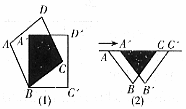
(1)请你仿照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形,并按图(4)中给出的正方形和正三角形的大小大致画出密铺后图形的示意图(只要画出一种图形即可):
(2)如果用形状、大小相同的如图(5)方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图。
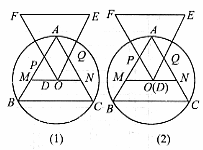
27. (本题9分)如图(1),已知圆O是等边△ABC的外接圆,过O点作MN//BC分别交AB、AC于M、N,且MN=a。另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、N重合),并始终保持EF//BC,DF交AB于点P,DE交AC于点Q。
(1)试判断四边形APDQ的形状,并进行证明;
(2)设DM为x,四边形APDQ的面积为y,试探究y与x的函数关系式;四边形APDQ的面积能取到最大值吗?如果能,请求出它的最大值,并确定此时D点的位置。
(3)如图(2),当D点和圆心O重合时,请判断四边形APDQ的形状,并说明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com