
2006年日照市中等学校招生考试
第Ⅰ卷
一、选择题:本题12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.第1~8题每小题选对得3分,第9~12题每小题选对得4分;选错、不选、或选出的答案超过一个,均记零分.
1.若点P(m,1-2m)的横坐标与纵坐标互为相反数,则点P一定在
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
2.已知小明家距离学校10千米,而小蓉家距离小明家3千米.如果小蓉家到学校的距离是d千米,则d满足
(A)3<d<10 (B)3≤d≤10 (C)7<d<13 (D)7 ≤d≤13
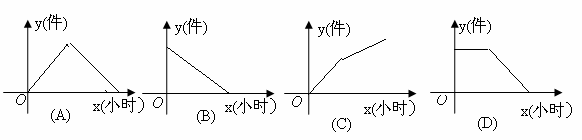
3.某海产品深加工厂的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时可以装产品150件,则未装箱的产品数y(件)是时间t(小时)的函数,这个函数的大致图像可能是
4.如图,在△ABC中,AB=AC,D为AC边上一点,且BD=BC=AD, 则∠A等于
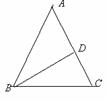
(A)30o(B)36o (C)45o (D)72o
5.已知方程组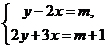 的解x、y满足2x+y≥0,则m的取值范围是
的解x、y满足2x+y≥0,则m的取值范围是
(A)m≥-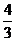 (B)m≥
(B)m≥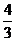 (C)m≥1(D)-
(C)m≥1(D)-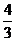 ≤m≤1
≤m≤1
6.AE、CF是锐角△ABC的两条高,如果AE:CF=3:2,则sinA:sinC等于
(A)3:2 (B)2:3 (C)9:4 (D)4:9
7.已知直线y=mx-1上有一点B(1,n),它到原点的距离是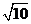 ,则此直线与两坐标轴围成的三角形的面积为
,则此直线与两坐标轴围成的三角形的面积为
(A)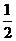 (B)
(B)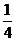 或
或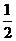 (C)
(C)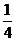 或
或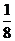 (D)
(D) 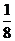 或
或 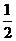
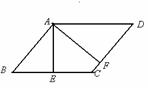
8.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B 两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1,则点C的个数为
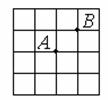
(A)3个 (B)4个 (C)5个 (D)6个
9.已知M、N两点关于y轴对称,且点M在双曲线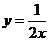 上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x
上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x
(A)有最小值,且最小值是 (B)有最大值,且最大值是-
(B)有最大值,且最大值是-
(C)有最大值,且最大值是 (D)有最小值,且最小值是-
(D)有最小值,且最小值是-
10.某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告.15秒的广告每播一次收费0.6万元,30秒的广告每播一次收费1万元.若要求每种广告播放不少于2次,则电视台在播放时收益最大的播放方式是
(A)15秒的广告播放4次,30秒的广告播放2次
(B)15秒的广告播放2次,30秒的广告播放4次
(C)15秒的广告播放2次,30秒的广告播放3次
(D)15秒的广告播放3次,30秒的广告播放2次
11.已知实数a、b、c满足:a<0,a-b+c>0,则一定有
(A)b2-4ac>0(B)b2-4ac≥0(C)b2-4ac≤0(D)b2-4ac<0
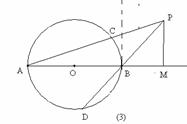
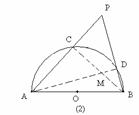
12.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连结AC、BC、OC,那么下列结论中:①PC2=PA?PB;②PC?OC=OP?CD;③OA2=OD?OP.正确的有
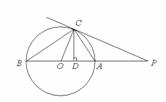
(A)0个 (B)1个 (C)2个 (D)3个
第Ⅱ卷
二、填空题:本题共5小题,每小题填对得3分,共15分.只要求填写最后结果.
13.某电脑公司在5月1日将500台电脑投放市场,经市场调研发现,该批电脑每 隔10天平均日销售量减少2台,现准备用38天销售完该批电脑,则预计该公司5月1日至5月10日的平均日销售量是 台.
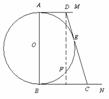
14.如图,⊙O的直径AB=12,AM和BN是它的两条切线,切点分别为A、B,DE切⊙O于E,交AM于D,交BN于C,设AD=x,BC=y,则y与x的函数关系式是 .
15.已知,关于x的方程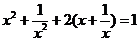 ,那么
,那么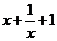 的值为
.
的值为
.
16.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45o,且AE+AF=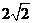 ,则平行四边形ABCD的周长是 .
,则平行四边形ABCD的周长是 .
17.德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数):
第一行
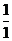
第二行
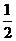
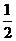
第三行
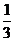
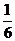
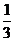
第四行
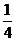
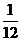
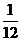
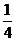
第五行
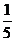
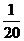
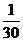
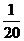
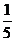
… …… ……
根据前五行的规律,可以知道第六行的数依次是: .
三、解答题:本题共7小题,共65分.解答时应写出文字说明、证明过程或演算步骤.
18.(本题满分8分)
下表是某市4所中学举行男子足球单循环赛的成绩登记表.表中①与②表示的是同一场比赛,在这场比赛中一中进了3个球,三中进了2个球,即一中以3:2胜三中,或者说三中以2:3负于一中,其余依次类推.按照比赛规则胜一场得3分,平一场得1分,负一场得0分.
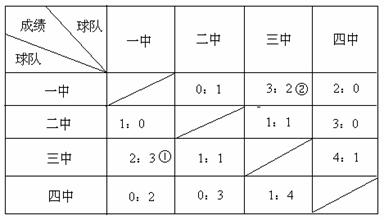
(1)本次足球单循环赛共进行了几场比赛?你能排出他们的名次吗?
(2)求各场比赛的平均进球数;
(3)求各场比赛进球数的众数和中位数.
19.(本题满分8分)
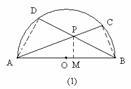
如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.
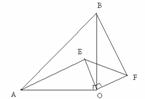
求证:(1)AE=BF;(2)AE⊥BF.
20.(本题满分9分)
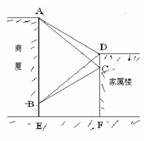
如图,“五一”期间在某商贸大厦上从点A到点B悬挂了一条宣传条幅,小明和小雯的家正好住在商贸大厦对面的家属楼上.小明在四楼D点测得条幅端点A的仰角为30o,测得条幅端点B的俯角为45o;小雯在三楼C点测得条幅端点A的仰角为45o,测得条幅端点B的俯角为30o.若设楼层高度CD为3米,请你根据小明和小雯测得的数据求出条幅AB的长.(结果精确到个位,参考数据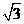 =1.732)
=1.732)
21.(本题满分10分)
在我市南沿海公路改建工程中,某段工程拟在30天内(含30天)完成.现有甲、乙两个工程队,从这两个工程队资质材料可知:若两队合做24天恰好完成;若两队合做18天后,甲工程队再单独做10天,也恰好完成.请问:
(1)甲、乙两个工程队单独完成该工程各需多少天?
(2)已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,甲、乙两队各做多少天(同时施工即为合做)?最低施工费用是多少万元?
22.(本题满分10分)
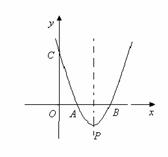
如图,已知抛物线与x轴交于A(m,0)、B(n,0)两点,与y轴交于点C(0, 3),点P是抛物线的顶点,若m-n= -2,m?n =3.
(1)求抛物线的表达式及P点的坐标;
(2)求△ACP的面积S△ACP.
23.(本题满分10分)
日照市是中国北方最大的对虾养殖产区,被国家农业部列为对虾养殖重点区域;贝类产品西施舌是日照特产.沿海某养殖场计划今年养殖无公害标准化对虾和西施舌,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表: (单位:千元/吨)
品种
先期投资
养殖期间投资
产值
西施舌
9
3
30
对虾
4
10
20
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.设西施舌种苗的投放量为x吨
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com